Relevant definitions:
“A set that is either finite or has the same cardinality as the set of positive integers is called countable. A set that is not countable is called uncountable. When an infinite set S is countable, we denote the cardinality of S by א0 (where א is aleph, the first letter of the Hebrew alphabet). We write |S| = א0 and say that S has cardinality aleph null.”
“The function f is a one-to-one correspondence, or a bijection, if it is both one-to-one and onto. We also say that such a function is bijective.”
HILBERT’S GRAND HOTEL “We now describe a paradox that shows that something impossible with finite sets may be possible with infinite sets. The famous mathematician David Hilbert invented the notion of the Grand Hotel, which has a countably infinite number of rooms, each occupied by a guest. When a new guest arrives at a hotel with a finite number of rooms, and all rooms are occupied, this guest cannot be accommodated without evicting a current guest. However, we can always accommodate a new guest at the Grand Hotel, even when all rooms are already occupied.”
The definitions above are from the textbook Discrete Mathematics and its Applications by Rosen.
To solve this exercise, we must find a bijection that assigns new rooms to the guests that are already in the hotel, and rooms to each of the arriving guests.
We can choose different bijections. Here, I’ll give you two of them and I encourage you to find two more.
For the first one, we are going to use the same bijection used to prove that the set of rational numbers is countably infinite. See the picture below.
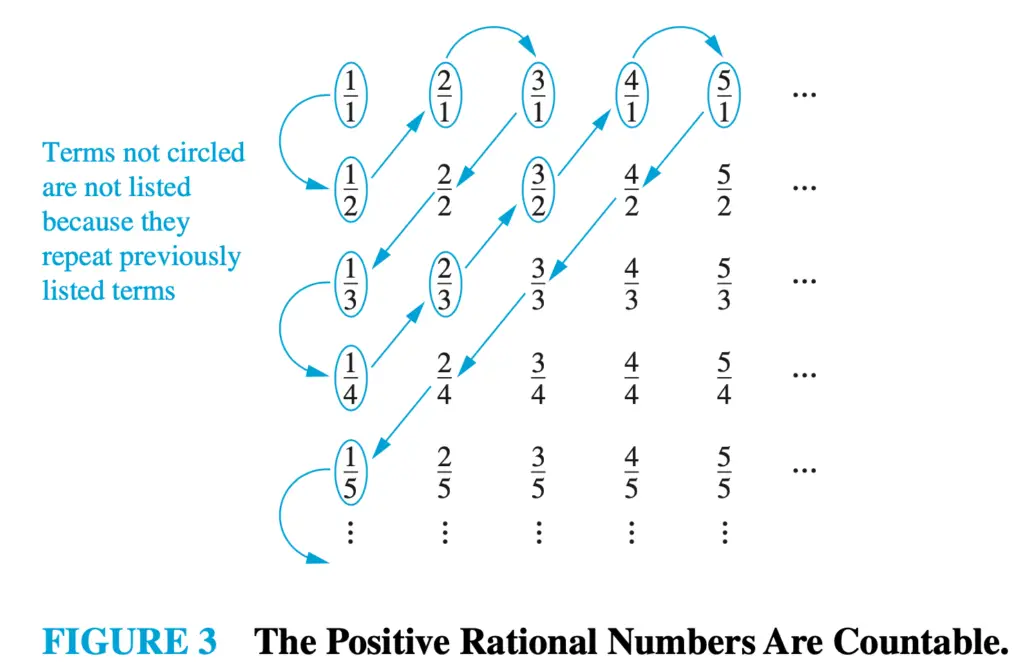
The first row in the picture above will represent the current guests. As the Grand Hotel is fully occupied, we have guests in rooms 1, 2, 3, … (numbered by the numerator). When the denominator (also the same as the row) is 1, it means the guests that are already at the Grand Hotel. For instance, 2/1 means the guest in room 2 that is currently in the hotel.
When the denominator d is greater than 1, it represents the bus d-1. For instance, 4/2 represents the person in sit 4, in the bus 2-1=1.
If we assign the rooms in the Grand Hotel in the same order that the arrows indicate in the figure above, we have assigned 1 room to each new guest without evicting any current guests.
This is an example of a technique used for problem-solving. Modify the input of the new problem into the input of a problem you already know how to solve, and then you just solved the new problem.
A second way of answering this problem can be making use of the fact that are infinite prime numbers.
We can use the prime numbers to assign the rooms as follows:
- Guests at the hotel are moved to room 2n, where n is the current room number.
- Guest in bus 1, can be assigned to room 3n, where n is the current sit number in the bus.
- Guest in bus 2, can be assigned to room 5n, where n is the current sit number in the bus.
- Guest in bus 3, can be assigned to room 7n, where n is the current sit number in the bus.
- And for each bus, we will use the next prime number.
Notice that a prime number is not divisible by any number other than 1 and itself. Therefore, there won’t be any collision in the assignment of the rooms when using powers of different prime numbers.
Are you ready to give your own two solutions?
Related exercises:
- 3. Determine whether each of these sets is countable or uncountable. For those that are countably infinite, exhibit a one-to-one correspondence between the set of positive integers and that set
- 4. Determine whether each of these sets is countable or uncountable. For those that are countably infinite, exhibit a one-to-one correspondence between the set of positive integers and that set.
- 6. Suppose that Hilbert’s Grand Hotel is fully occupied, but the hotel closes all the even numbered rooms for maintenance. Show that all guests can remain in the hotel
- 7. Suppose that Hilbert’s Grand Hotel is fully occupied on the day the hotel expands to a second building which also contains a countably infinite number of rooms. Show that the current guests can be spread out to fill every room of the two buildings of the hotel
- 8. Show that a countably infinite number of guests arriving at Hilbert’s fully occupied Grand Hotel can be given rooms without evicting any current guest
