As we always do, let’s first start with the relevant definitions we need to solve this exercise.
“A set that is either finite or has the same cardinality as the set of positive integers is called countable. A set that is not countable is called uncountable. When an infinite set S is countable, we denote the cardinality of S by א0 (where א is aleph, the first letter of the Hebrew alphabet). We write |S| = א0 and say that S has cardinality aleph null.”
“The function f is a one-to-one correspondence, or a bijection, if it is both one-to-one and onto. We also say that such a function is bijective.”
The definitions above are from the textbook Discrete Mathematics and its Applications by Rosen.
a) all bit strings not containing the bit 0
The set of all bit strings can have as many bits as integer numbers are there. Therefore, this set is countable infinity.
The one-to-one correspondence is easy to show. It is the function that assigns to a bit string, the number of 1s in that string.
You can see that this function is one-to-one, as is not possible for the same bit string to have two different number of 1s.
The function is also onto because the range is the set of positive integers. For each positive number, you can find a related value in the domain that will be the bit string with that specific number of 1s.
Therefore, the function is a one-to-one correspondence with the set of positive integers.
b) all positive rational numbers that cannot be written with denominators less than 4
We already know, by Example 4 from the textbook, the set of positive rational numbers is countably infinite. The one-to-one correspondence is shown in the picture below. Notice that they can be listed in the sequence specified in the picture.
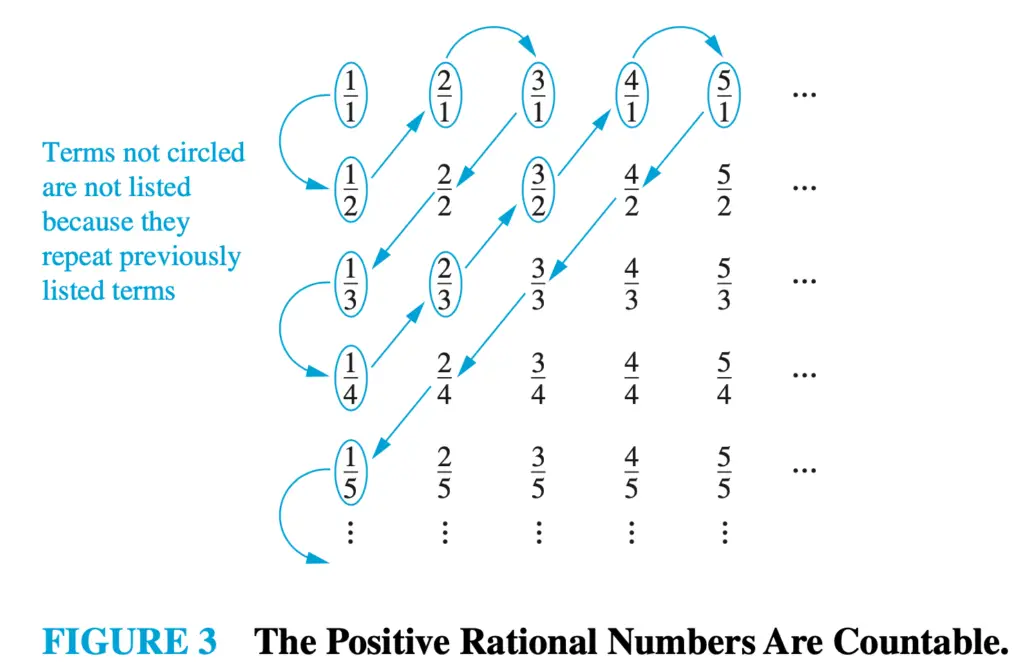
Following a similar approach, we write those numbers in the same way as in the picture above. But in this case, we omit the first four rows as this set does not contain rational numbers with denominators less than 4.
Therefore, this set is countably infinite.
c) the real numbers not containing 0 in their decimal representation
Uncountable.
d) the real numbers containing only a finite number of 1s in their decimal representation
Uncountable.
Related exercises:
- 4. Determine whether each of these sets is countable or uncountable. For those that are countably infinite, exhibit a one-to-one correspondence between the set of positive integers and that set.
- 6. Suppose that Hilbert’s Grand Hotel is fully occupied, but the hotel closes all the even numbered rooms for maintenance. Show that all guests can remain in the hotel
- 7. Suppose that Hilbert’s Grand Hotel is fully occupied on the day the hotel expands to a second building which also contains a countably infinite number of rooms. Show that the current guests can be spread out to fill every room of the two buildings of the hotel
- 8. Show that a countably infinite number of guests arriving at Hilbert’s fully occupied Grand Hotel can be given rooms without evicting any current guest
- ∗9. Suppose that a countably infinite number of buses, each containing a countably infinite number of guests, arrive at Hilbert’s fully occupied Grand Hotel. Show that all the arriving guests can be accommodated without evicting any current guest
