General Tree Data Structure: implementation and usage in Java

The General Tree data structure is one of the classic data structures studied in a Data Structure and Algorithms course. You will learn here how to implement the general tree data structure.

So, let’s start by stating what do we mean by General Tree.

General Tree Definition
ADT General Tree
General Tree Data Structure Traversals Operations
- Pre-order
- In-order
- Post-order
- Example
General Tree data structure implementation
Example on how to use the General Tree implementation
- Utility class TreeUtils
- General Tree Data Structure: Example of Console Application
Summary

General Tree Definition

A tree is a mathematical model. Therefore, it is defined in Discrete Mathematics as: ” A tree is a connected undirected graph with no simple circuits.” Source Discrete Mathematics and its Applications by Rosen.

However, for implementation purposes, it is better to use a recursive definition that is closer to Computer Science.

A node is a tree. That node is also the root of the tree.
If r is a node and T1, T2, …, Tk are subtrees with roots r1, r2, …, rk; we can create a new tree where r will be the parent of the nodes r1, r2, …, rk. In the new tree r is the root and T1, T2, …, Tk are subtrees of the root. We say that the nodes r1, r2, …, rk are children of node r.
Sometimes is useful to have the null tree. This is a tree without nodes.

The previous definition is usually known as General Tree.

Notice from the definition above, that a tree is a non-linear data structure. It is mainly used to model hierarchical data, although it has other uses, like to create faster-searching algorithms.

A tree in which all nodes have a maximum of 2 children, is called a binary tree. In the same way, a tree in which all nodes have a maximum of 3 children is called a ternary tree.

There are other types of trees, but those are classified according to the way that they are created and the data they hold in the nodes. Those are out of the scope of this post.

ADT General Tree

The ADT tree has the following general operations:

T Root(); // returns the root of the tree
boolean isLeaf(); //return true if the tree does not have children
int numberSubTrees(); // return the number of subtrees associated
ITree<T> getSubTree(int i); //return the ith subtree of the tree
void addSubTree(ITree<T> subtree);
List<T> preorder(); // return the nodes in pre-order
List<T> inorder(); // return the nodes in in-order
List<T> postorder(); // return the nodes in post-order

Here it is better to you use generics (The type T as a parameter or return type). This allows you to create trees that can hold different types in the nodes but using the same implementation.

In Java, we can define these operations in an interface. Then, we implement different types of trees.

public interface ITree<T> {
    T Root(); 
    boolean isLeaf(); 
    int numberSubTrees(); 
    ITree<T> getSubTree(int i); 
    void addSubTree(ITree<T> subtree);
    List<T> preorder();
    List<T> inorder();
    List<T> postorder();
    int Height();
}

In this article, I’ll show you only the implementation of a General Tree.

General Tree Data Structure Traversals Operations

With disregard of the type of tree you are implementing, the most important operations are the traversals operations.

The reason behind this is that those are like the basic algorithms for trees. Most of the problems that are modeled and solved using trees need a traversal as the core of the solution.

Pre-order

From the tree definition, you know that the tree has a root and several (or none) subtrees. The subtrees at the same time have a root and several (or none) subtrees, and so on.

A tree without subtrees is known as a leaf.

We do a preorder traversal as follows:

First, we visit (print) the root.
Then, we visit all the subtrees in preorder.

Because we recursively defined the tree, it will make it easier to understand the traversals.

In-order

In this case, the steps are as follows:

First, the left-most child is visited (printed).
Then, we visit (print) the root of the tree.
After that, we visit the rest of the children in in-order.

Post-order

In this case, the steps are as follows:

First, we visit all the subtrees in preorder.
Then, we visit (print) the root of the tree.

Example

Consider the tree from the following figure.

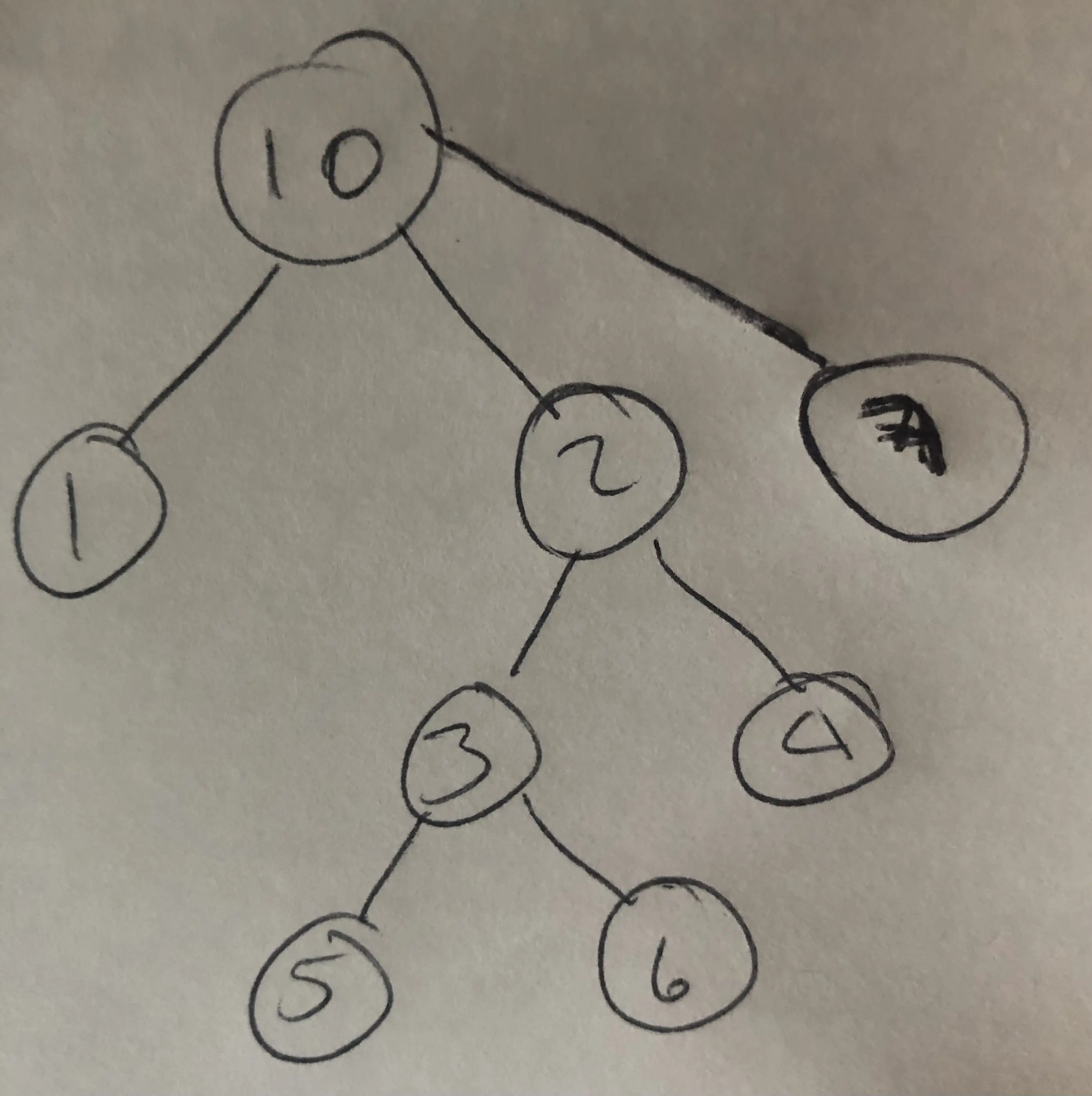
The traversals will be as follows:

preorder: 10, 1, 2, 3, 5, 6, 4, 7
inorder: 1, 10, 5, 3, 6, 2, 4, 7
postorder: 1, 5, 6, 3, 4, 2, 7, 10

General Tree data structure implementation

Let’s see our Java implementation for the class GeneralTree.

public class GeneralTree<T> implements ITree<T>{
    private T root;
    private LinkedList<ITree<T>> children;

    GeneralTree(T root){
        this.root = root;
        children = new LinkedList<>();
    }
    @Override
    public T Root() {
        return root;
    }

    @Override
    public boolean isLeaf() {
        return children.isEmpty();
    }

    @Override
    public int numberSubTrees() {
        return children.size();
    }

    @Override
    public ITree<T> getSubTree(int i) {
        return children.get(i);
    }

    @Override
    public void addSubTree(ITree<T> subtree) {
        children.add(subtree);
    }


    @Override
    public List<T> preorder() {
        return _preorder(new LinkedList<>());
    }

    private List<T> _preorder(List<T> result){
        result.add(root);
        if (!isLeaf()){
            for (ITree<T> subtree: children) {
                ((GeneralTree)subtree)._preorder(result);
            }
        }
        return result;
    }

    @Override
    public List<T> inorder() {
        return _inorder(new LinkedList<>());
    }

    private List<T> _inorder(List<T> result){
        if (isLeaf()) {
            result.add(root);
        }
        else{
            ((GeneralTree)children.get(0))._inorder(result);
            result.add(root);
            for (int i=1; i<numberSubTrees(); i++) {
                ((GeneralTree)children.get(i))._inorder(result);
            }
        }
        return result;
    }

    @Override
    public List<T> postorder() {
        return _postorder(new LinkedList<>());
    }



    private List<T> _postorder(List<T> result){
        for (int i=0; i<numberSubTrees(); i++) {
            ((GeneralTree)children.get(i))._postorder(result);
        }
        result.add(root);
        return result;
    }

    @Override
    public int Height() {
        if(isLeaf())
            return 0;
        int max = 0;
        for (int i = 0; i < children.size(); i++)
        {
            int h = children.get(i).Height();
            if(max < h)
                max = h;
        }
        return max+1;
    }
}

Example on how to use the General Tree implementation

First, let’s implement a utility class that prints the tree in the console in a way that we can see the tree structure.

Utility class TreeUtils

Find below the implementation of the class TreeUtils.

class TreeUtils{
    public static <T> void printTreeToConsole(ITree<T> tree, String indent) {
        System.out.println(indent + tree.Root());
        indent += "|-  ";

        for (int i = 0; i < tree.numberSubTrees(); i++)
            printTreeToConsole(tree.getSubTree(i), indent);
    }
}

Notice that we are using a generic method. In other words, we are passing the type of information contained in tree nodes as a parameter. In this way, we can work with trees that hold different information.

General Tree Data Structure: Example of Console Application

Let’s create the same tree that is in the figure below, used as an example of traversals.

public class TreesExample {
    public static void main(String[] args){
        GeneralTree<String> tree = new GeneralTree<>("10");
        GeneralTree<String> subtree1 = new GeneralTree<>("1");
        GeneralTree<String> subtree2 = new GeneralTree<>("2");
        GeneralTree<String> subtree3 = new GeneralTree<>("3");
        GeneralTree<String> subtree4 = new GeneralTree<>("4");
        GeneralTree<String> subtree5 = new GeneralTree<>("5");
        GeneralTree<String> subtree6 = new GeneralTree<>("6");
        GeneralTree<String> subtree7 = new GeneralTree<>("7");

        subtree2.addSubTree(subtree3);
        subtree2.addSubTree(subtree4);
        subtree3.addSubTree(subtree5);
        subtree3.addSubTree(subtree6);
        tree.addSubTree(subtree1);
        tree.addSubTree(subtree2);
        tree.addSubTree(subtree7);

        List<String> preoderList = tree.preorder();
        System.out.println("preoder:");
        printList(preoderList);
        List<String> inorderList = tree.inorder();
        System.out.println("inoder:");
        printList(inorderList);
        List<String> postorderList = tree.postorder();
        System.out.println("postoder:");
        printList(postorderList);
        System.out.println("Tree structure:");
        TreeUtils.printTreeToConsole(tree,"");
    }
    static <T> void printList(List<T> list){
        for(T elem: list){
            System.out.print(elem + ", ");
        }
        System.out.println();
    }
}

Here, I also created a utility method, also known as helpers, to print a list of elements. This will help us to see the result of the traversals.

After executing this console application, we will get the following result.

Summary

A tree ADT is useful to model and work with hierarchical data.

It is very important to understand the traversals algorithms because they are the basis for solving problems using the ADT Tree.

H@ppy coding!

Table of Contents