As usual, to solve this type of exercise we should look at the logical operators. In this case, we only have negation (¬), so let’s start by having the truth table for that specific operator.
Truth table for the negation (¬) of a proposition
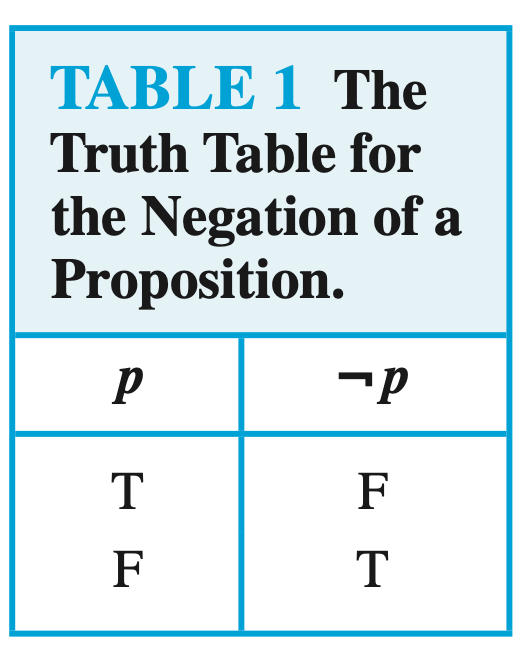
Solution to the exercise
If we analyze what we have to prove, we can see that there is only one propositional variable (p). Also, you can see that there are two compound propositions involved: ¬p and ¬(¬p).
So, we will have a table with three columns (p, ¬p, ¬(¬p)) and two rows for the two possible truth values of the propositional variable.
| p | ¬p | ¬(¬p) |
| T | F | T |
| F | T | F |
Using the truth table for the negation of a proposition (see picture above), we can complete the truth table.
After completing the truth table, we can state that p and ¬(¬p) are logically equivalent because they have the same truth values.
Related posts:
- What are propositional equivalences in Discrete Mathematics?
- Use truth tables to verify these equivalences (Ex. 1. pp. 34 from the textbook)
- Use truth tables to verify the associative laws (Ex. 4 pp. 34 from the textbook)
- Use a truth table to verify the first De Morgan law (Ex. 6 pp. 34 from the textbook)
- Show that p → q and ¬q → ¬p are logically equivalent (Ex. 18 pp. 35 from the textbook)
- Show that p↔ q and (p∧q)∨(¬p∧¬q) are logically equivalent
