To prove the first De Morgan law, we need to use the truth table for conjunctions, disjunctions, and negation of propositions.
Truth tables for conjunction, disjunctions and negation
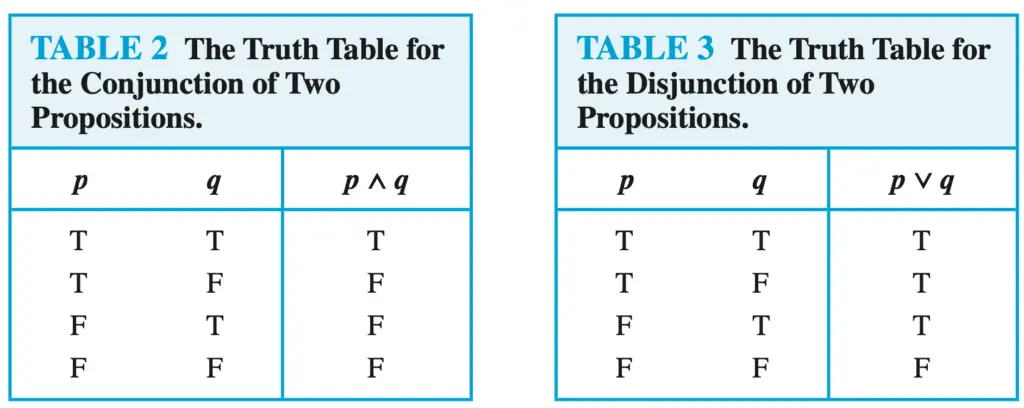
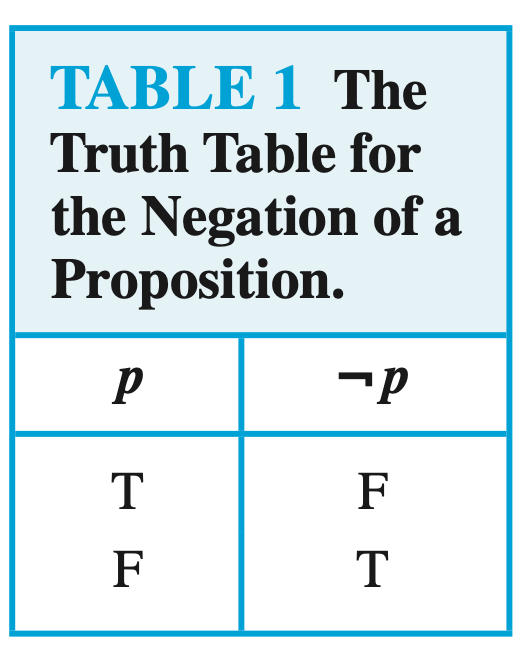
Now we can start solving the exercise.
First De Morgan Law
The following propositional equivalence is the First De Morgan Law.
¬(p ∧ q) ≡ ¬p ∨ ¬q
Using the same analysis as in previous exercises, we have two propositional variables and five compound propositions. This means the truth table will have 4 rows and 7 columns.
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | ¬p ∨ ¬q |
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
Notice that I used the truth table for the conjunction, disjunction, and negation of propositions.
For instance, in the first row:
- p ∧ q is T because p is T and q is T, and T∧T is T according to the truth table for the conjunction of two propositions.
- ¬p is F because P is T, and according to the truth table for the negation of a proposition, ¬T is F.
After creating the truth table above, we can state that ¬(p ∧ q) is logically equivalent to ¬p ∨ ¬q because they have the same truth values.
This proves the first De Morgan Law.
You mustn’t forget to state your conclusion after you create the truth table. Also, you need to justify that conclusion. The truth table by itself don’t prove anything.
Related posts:
- What are propositional equivalences in Discrete Mathematics?
- Use truth tables to verify these equivalences (Ex 1. pp. 34)
- Show that ¬(¬p) and p are logically equivalent (Ex 2. pp. 34)
- Use truth tables to verify the associative laws (Ex. 4 pp. 34)
- Show that p → q and ¬q → ¬p are logically equivalent (Ex 18 pp 35)
- Show that p↔ q and (p∧q)∨(¬p∧¬q) are logically equivalent
