To solve this exercise, we have to options.
We can answer using a state table or state diagram.
First, we need to consider that to be in the final state, we need first to start from S0, and recognize a 0, and then a 1. This tells us that we should have at least three states. S0 is the initial state, S1 is the state where we already recognized a 0, and S2 is a state where we first recognized a 0 and then a 1. Therefore, S2 will be a final state.
Let’s see how the final automata will looks like.
| f | ||
| State | 1 | 0 |
| S0 | S1 | |
| S1 | S2 | |
| S2 | S2 | S2 |
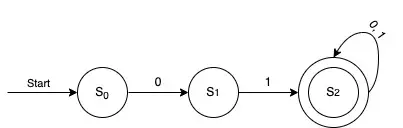
Notice that in both cases, strings starting with 01 are recognized.
We have the initial state S0 and a normal state S1. The only way to be in the state S2 is if the first input bit was 0 and the second one was 1.
After that, no matter what comes next, we stay in the final state S2. Therefore, the automaton recognizes any bit string that starts with 01.
You can use any of the two representations. Just remember if you are using a state table, to specify what is (are) the final state (s).
Similar exercises:
