In this post, I’ll show you an example of how to calculate the practical time complexity of two algorithms that solve the same problem.
As you should remember from the previous post, we calculate temporal complexity to assess how efficient an algorithm is compared to another algorithm. By doing this, we can choose the best algorithm among several.
To calculate this type of temporal complexity, we need an algorithm already implemented in a particular programming language, python in this case.
Two algorithms
In this case, we will use two algorithms that receive as input a number and return whether the number is prime or not.
In case you don’t remember, a prime number is a number that has only two divisors: 1 and itself. These numbers are very important, in particular in Cryptography.
So, to find out if a number is prime, there are several algorithms, and I’ll compare only two of them.
def is_prime(n):
square_root = int(n**0.5) + 1
for i in range(2, square_root):
if n % i == 0:
return False
return True
def is_prime1(n):
for i in range(2, n-1):
if n % i == 0:
return False
return True
The difference between the algorithms above is the number of iterations in the for loop. But both algorithms are correct. I leave the correctness proof of these two algorithms to the reader.
What are the variables that influence the practical temporal complexity?
The variables that influence the results are:
- Programming language
- The specific implementation of the algorithm
- Hardware that runs the algorithm
In our case, we are using Python as a programming language. The two specific implementations are in the section above.
The hardware specification is as follows:
- Macbook Pro 13’ 2017
- 2.3 GHz dual-core intel core i5
- 8 Gb 2133 MHz ram
- MacOS 13.6
The calculation of practical temporal complexity is an experiment (in terms of research). Because of this, we need to make sure we are giving all important details so other people can reproduce the experiment.
Results
To test both algorithms, we are going to create two separate programs and execute them using the same input.
For the input, I chose the prime number 15485863, which I already know is prime.
See below the code that I used to call the two functions.
if __name__=='__main__':
n = int(input('Enter a number greater than 1: '))
if n>1:
print('It is prime') if is_prime(n) else print('It is not prime')
To call the second implementation, I change is_prime(n) by is_prime1(n).
When executing the first algorithm, I got the following result.
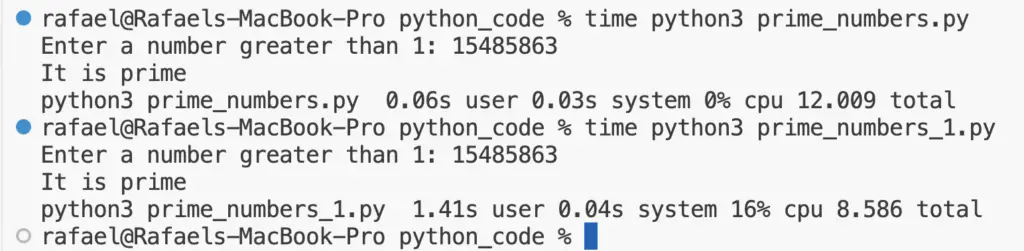
% time python3 prime_numbers.py
Enter a number greater than 1: 15485863
It is prime
python3 prime_numbers.py 0.06s user 0.03s system 0% cpu 12.009 total
Notice that when you use the command time before the execution of the program, you get the execution time of the program. In this case, the program took 0.06 seconds to run.
Let’s examine the second one.
% time python3 prime_numbers_1.py
Enter a number greater than 1: 15485863
It is prime
python3 prime_numbers_1.py 1.41s user 0.04s system 16% cpu 8.586 total
The second one took 1.41 seconds to run. That is 23.5 more time than the first implementation.
With this, we can say that from these two particular solutions to the same problem, the first one is the efficient solution.
Tips
There are certain things we can do to make this type of result more reliable.
Below are some tips you can use:
- Test using several inputs, with different sizes.
- Run the program several times, remove the biggest and smallest time, and calculate an average of the rest. Using that average is better as it can take care of fast/slower times because of process allocations in the operating system and other reasons.
- Make sure you document everything.
- If you are doing this for a research report or a thesis, after you write this part of the report, run again the test following the description you wrote, and compare the results. They are not going to be the same, but they should be close.
Next, you should learn what is the Big-O notations. It is important because it is the notation we use to calculate the theoretical temporal (or spatial) complexity of an algorithm.
I encourage you to try the two implementations above on your computer and leave me a comment below on the results you got.

