Propositional Logic: Exercise 6

The purpose of this post is to explain how to solve this type of exercise.

Suppose that Smartphone A has 256 MB RAM and 32 GB ROM, and the resolution of its camera is 8 MP; Smartphone B has 288 MB RAM and 64 GB ROM, and the resolution of its camera is 4 MP, and Smartphone C has 128 MB RAM and 32 GB ROM, and the resolution of its camera is 5 MP. Determine the truth value of each of these propositions.

a)  Smartphone B has the most RAM of these three smartphones.

b)  Smartphone C has more ROM or a higher resolution camera than Smartphone B.

c)  Smartphone B has more RAM, more ROM, and a higher resolution camera than Smartphone A.

d)  If Smartphone B has more RAM and more ROM than Smartphone C, then it also has a higher resolution camera.

e)  Smartphone A has more RAM than Smartphone B if and only if Smartphone B has more RAM than Smartphone A.

In this type of exercise, every time you want to answer one question, you will have to read the whole statement again to find out what the RAM on each phone is, what is the ROM, and so on.

This can take time, and, in some cases, it can confuse you.

What works for me, is to summarize the information as follows:

Now, the information we need about smartphones is easily accessible.

Before you start answering these questions, you should know the truth values for conjunctions, disjunctions, conditionals, and biconditionals. I summarized them below.

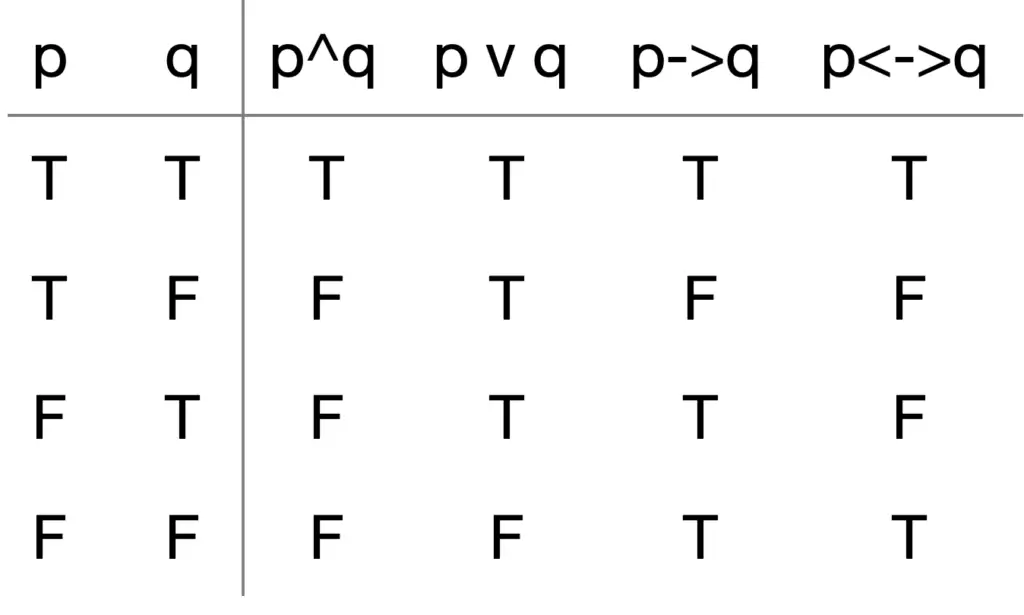
Now you are ready to answer each question.

a) Smartphone B has the most RAM of these three smartphones.

It is easy to see that the answer is True. Notice that the RAM of smartphone B is 288>256>128.

b) Smartphone C has more ROM or a higher resolution camera than Smartphone B.

Now, let’s substitute the values on the proposition.

(32 GB > 64 GB) or (5 MP > 4 MP) = False or True = True

c) Smartphone B has more RAM, more ROM, and a higher resolution camera than Smartphone A.

In this case, we proceed the same way that the previous question.

(288 MB > 256 MB) ^ (64GB > 32 GB) ^ (4 MP > 8 MP) = True ^ True ^ False = False

d) If Smartphone B has more RAM and more ROM than Smartphone C, then it also has a higher resolution camera.

In this case, the compound proposition will be as follows:

((288 MB > 128 MB) ^ (64 GB > 32 GB)) -> (4 MP > 5 MP)

T ^ T -> F

T -> F

False

e) Smartphone A has more RAM than Smartphone B if and only if Smartphone B has more RAM than Smartphone A.

(256 GB > 288 MB) <-> (288 MB > 256 GB)

F <-> T

Notice that according to the truth table for the biconditional (see the picture above), the result will be True only when both sides are either True or both are False. In other words, when both sides have the same truth value.

By using the truth table for the biconditional, you can see the answer, in this case, is False. However, you can also find the result as follows.

F <-> T

(F->T) ^ (T->F), notice that p <-> p has the same truth value than (p->q) ^ (q->p)

T ^ F

F

Related topics:

• Propositional Logic: Exercise 7 from the textbook. Suppose that during the most recent fiscal year, the annual revenue of Acme Computer was 138 billion dollars …
• What is the negation of each of these propositions?
• Negating propositions
• Which of these sentences are propositions? What are the truth values of those that are propositions?
• Propositional logic Exercise 11. Write these propositions using p and q and logical connectives (including negations)
• For each of these sentences, state what the sentence means if the logical connective or is an inclusive or (that is, a disjunction) versus an exclusive or. Which of these meanings of or do you think is intended?