Construct a deterministic finite-state automaton that recognizes the set of all bit strings that contain exactly three 0s.

We will follow a similar approach to previous exercises to solve this exercise.

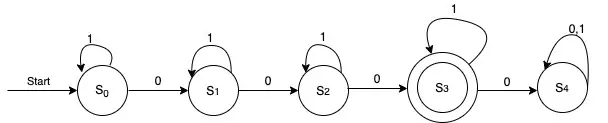
Let’s define 5 states as follows:

S₀, the initial state
S₁ is the state when the automata read exactly one 0
S₂ is the state when the automata read exactly two 0s
S₃ is the state when the automata read exactly three 0s. This is our final state because the automaton should recognize only strings with exactly three 0s.
S₄ is the state when the automaton read more than three 0s.

After the definition of the previous states, we can also define the following transitions:

From the initial state with a 1, there is no need to change to a different state.
Reading a 0 at the initial state, the new state will be S₁ (the automaton read exactly one 0).
At S₁, reading a 0, the automaton will go to the next state S₂ (the automaton read exactly two 0s).
At S₁, reading a 1, the automaton will stay in the same state.
At S₂, reading a 0, the automaton will go to the state S₃. The automaton read exactly three 0s. Therefore, this one is a final state.
At S₂, reading a 1, the automaton will stay in the same state.
At S₃, reading a 0, the automaton will go to the state S₄. At this point, the string cannot be recognized by this automaton. Therefore, this state is not final and whatever bit comes next, the automaton will stay in the same state.

A deterministic finite-state automaton that recognizes the set of all bit strings that contain exactly three 0s

We can also specify the transition function using the table below. Don’t forget to specify that S₃ is the final state if you use a state table.

	f
States	1	0
S₀	S₀	S₁
S₁	S₁	S₂
S₂	S₂	S₃
S₃	S₃	S₄
S₄	S₄	S₄

Transition function, using a state table, for a deterministic finite-state automaton that recognizes the set of all bit strings that contain exactly three 0s

Similar exercises: