We will follow a similar approach to previous exercises to solve this exercise.
Let’s define 4 states as follows:
S0, the initial state
S1 is the state when the automata read a 1
S2 is the state when the automata read a 0 after a 1
S3 is the state when the automata read a 1 after reading 01. This will be the final state.
After the definition of the previous states, we can also define the following transitions:
- From the initial state with a 1, the new state will be S1 (the state when the automata read a 1).
- Reading a 0 at the initial state, there is no need to change to a different state.
- At S1, reading a 0, the automaton will go to the next state S2 (reading 0 after a 1).
- At S2, reading a 1, the automaton will go to the final state S3 (reading a 1 after a 10)
- At S2, reading a 0, the automaton should be in the initial state. Because the sequence 101 is now “broken”. So, at the initial state, we can start recognizing sequence 101 again.
- If at state S3, it means that the sequence 101 was already recognized. At this stage, the automaton can read 0s or 1s and still recognize/accept the string. That is why if it reads 0 or 1 just stay in the same state.
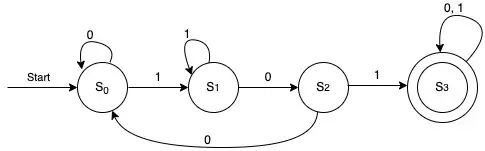
We can also specify the transition function using the table below. Don’t forget to specify that S3 is the final state if you use a state table.
| f | ||
| States | 1 | 0 |
| S0 | S1 | S0 |
| S1 | S1 | S2 |
| S2 | S3 | S0 |
| S3 | S3 | S3 |
Similar exercises:
