This exercise is a bit more difficult than the previous one.
To solve this exercise, let’s use the following strategy: define states in which the automaton can be if it just reads a 1 or a 0.
– We can have a state S1 which means the automaton read 0s. Therefore, from the state S0 with a 0, the automaton goes to state S1. And in the state S1, if we read a 0, the machine stays in the same state. Because it is the state that tells us that we just read a 0.
– Another state S2, means we just read a 1. So, at S1, reading a 1, the machine transition to the state S2. Form S0, reading a 1, we also move to state S2. Because S2 is the state that means we just read a 1.
– Lastly, we need an extra state S3. It will be a final state. And we can only get to that state if we are at S2 (where we just read a 1) and we read a 0 (the strings ending with 10).
– After that, we check that every state does something when reading a 1 or a 0.
Find the state diagram below.
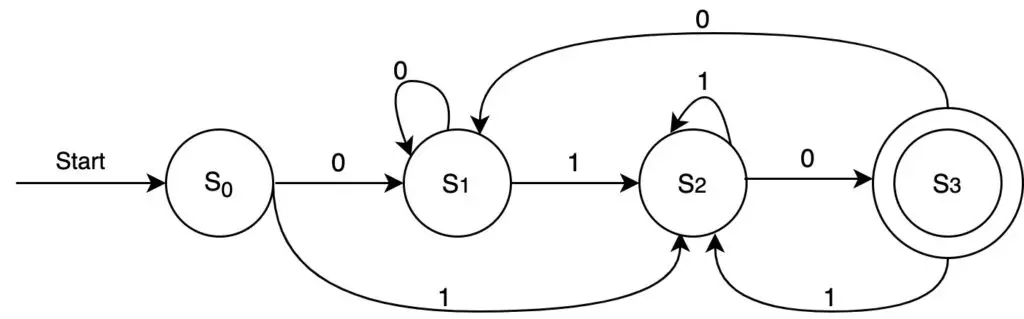
Notice that, at the state S3, reading a 0 should take the automata to the state S1. Because S1 is the state where you just read a 0. And, from S3 with a 1, the new state will be S2, because S2 is the state where we just read a 1.
We can also specify the transition function using the table below. Don’t forget to specify that S3 is the final state if use a state table.
| f | ||
| States | 1 | 0 |
| S0 | S2 | S1 |
| S1 | S2 | S1 |
| S2 | S3 | S2 |
| S3 | S1 | S2 |
automaton that recognizes the set of all bit strings that end with 10.
Similar exercises:
