This is an interesting type of exercise.
To make easier this exercise, let’s write an irreflexive relation, represent it using a matrix, and find out what are the characteristics of such a matrix.
But first, let’s refresh what an irreflexive relation is.
Definition: “A relation R on the set A is irreflexive if for every a ∈ A, (a, a) ∈/ R. That is, R is irreflexive if no element in A is related to itself.”
Let R={(1,2),(2,1), (3,1)} be a relation on the set A={1,2,3}.
We can state that R is irreflexive as there is no element a∈A such that (a,a)∈R.
Now, let’s see the matrix representation of R.
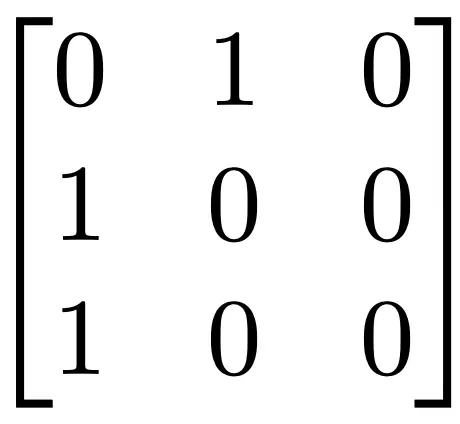
Notice that all elements in the diagonal of the matrix are 0.
Also, notice that if at least 1 element in the diagonal was 1, then at least one element of the set A will be related with itself by R. This will make the relation not irreflexive.
Answer:
The relation is irreflexive if and only if the main diagonal of the matrix does not contain any 1. In other words, if the main diagonal of the matrix contains only 0s.
Related exercises:
- How many nonzero entries does the matrix representing the relation R on A={1,2,3,…,100} consisting of the first 100 positive integers have if R is
- List the ordered pairs in the relations on {1, 2, 3} corresponding to these matrices (where the rows and columns correspond to the integers listed in increasing order).
- Represent each of these relations on {1, 2, 3} with a matrix (with the elements of this set listed in increasing order)
