a) {(a,b)|a>b}?
To answer this exercise, let’s find out how many 1s will have in each row. Then, we add them up.
The last row (row 100) will have ninety-nine 1s because 99 numbers are less than 100 in the set A={1,2,3,…,100}.
The second last row (row 99) will have ninety-eight 1s as 98 numbers are less than 99.
So, the pattern is that each row will have 1 number less than the index of the row.
So, the total number of 1s will be:
99+98+97+96+…+1
Now, how we can calculate the final value?
We know from the topic of sequences and summations, that one useful summation formula is the following:
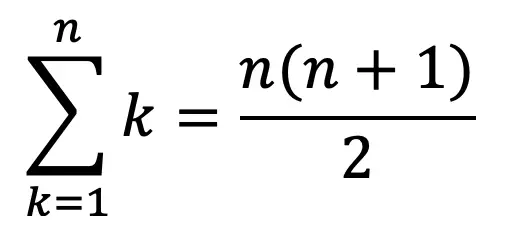
So,
99+98+97+96+…+1 = 1+2+3+…+99 = 99(99+1)/2=99×100/2=4950
Answer: 4950
b) {(a,b)|a≠b}?
In this case, we can see that there will be 0s only in the main diagonal (One hundred 0s).
So, we just subtract 100 from the total elements 10 000 and we get the answer.
Answer:
9900
c) {(a,b)|a=b+1}?
In this case, you can look at a smaller example. Let’s say, in a 5×5 matrix.
If you write the matrix, you will notice that the 1s are exactly under the main diagonal.
In other words, (1,2), (2,3), (3,4), and (4,5) are the ordered pairs that belong in the relation. That will be the number of rows-1, as (1,1) will never be part of this relation.
Answer: 99
d) {(a,b)|a=1}?
In this case, we know that all elements will be related to a=1. Also, we know that there are 100 elements in the set A. The relation will have the form:
R={(1,1), (1,2), (1,3), (1,4), …, (1,100)}
Answer: 100
e) {(a,b) | ab = 1}?
In the set of integers numbers from 1 to 100, there is only one pair that holds the condition ab=1.
The pair is (1,1).
Answer: 1
Related exercises:
- How can the matrix representing a relation R on a set A be used to determine whether the relation is irreflexive?
- List the ordered pairs in the relations on {1, 2, 3} corresponding to these matrices (where the rows and columns correspond to the integers listed in increasing order).
- Represent each of these relations on {1, 2, 3} with a matrix (with the elements of this set listed in increasing order)
