In this case, we are given the matrix that represents the relation, and we need to write the pairs that belong to the relation. It is the opposite of this exercise.
a) Matrix 1

The approach to solving this type of exercise is to find where there is a 1 in the matrix and write down the row and the column as an ordered pair.
Answer:
(1,1), (1,3), (2,2), (3,1), (3,3)
Make sure the number of ordered pairs is the same as the number of 1s in the matrix.
b) Matrix 2
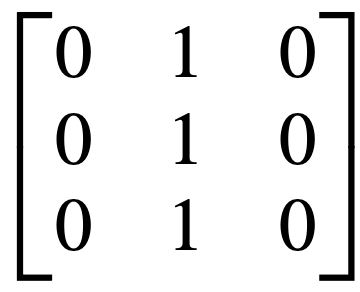
Answer:
(1,2), (2,2), (3, 2)
Notice in this case that all the 1s are in the same column (number 2). That is why “2” is the second element of all the ordered pairs in the relation R.
c) Matrix 3

Answer:
(1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (3, 3)
Related exercises:
- How many nonzero entries does the matrix representing the relation R on A={1,2,3,…,100} consisting of the first 100 positive integers have if R is
- How can the matrix representing a relation R on a set A be used to determine whether the relation is irreflexive?
- Represent each of these relations on {1, 2, 3} with a matrix (with the elements of this set listed in increasing order)
