The definitive example to learn recursion and backtracking: the maze problem

Recursion is a very important tool in programming. It is also difficult to understand. In this post, I want to show an example of a problem that can be solved with recursion and will help you understand how to use backtracking.

Backtracking is a useful technique we can use to verify all the possible solutions to a problem.

The main idea is as follows:

If I can take a step to solve the problem, I take it.
I take one step back (backtracking) and check for another step that can take me closer to the solution.
Repeat until there are no more steps to check.

Backtracking is an important technique we can use when solving a specific type of problems. You will easily identify those problems because for you to find the solution, you will have to explore all the possible solutions to the problem.

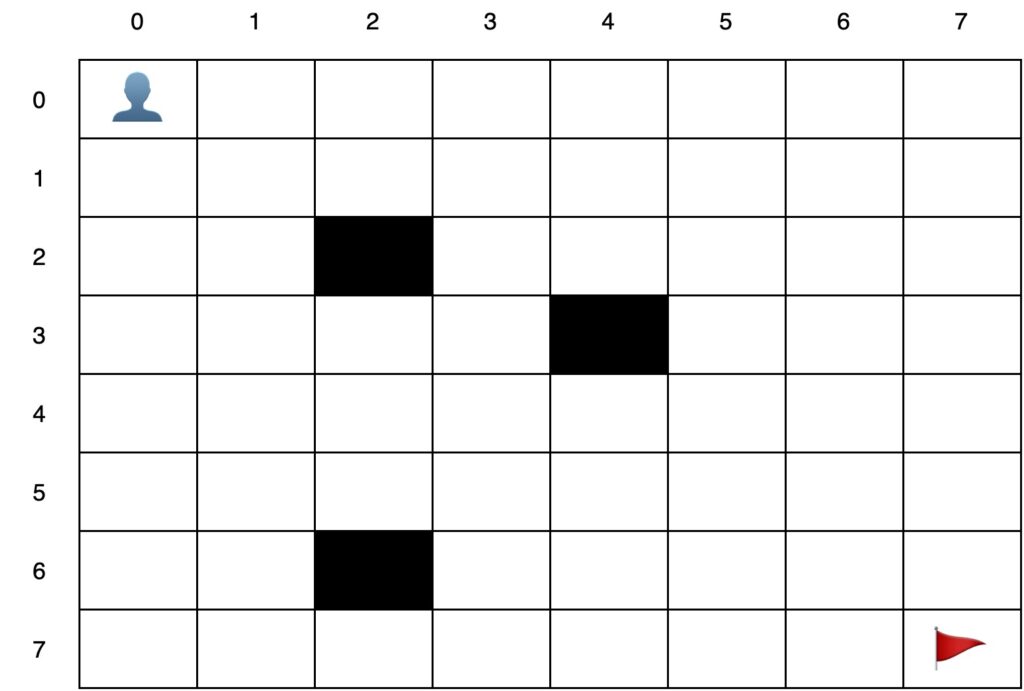
Problem examples: the maze problem

There are several solutions to the maze problem (see this link). Some of them depend on how we enunciate the problem.

In the scope of this article, and to show how backtracking works, we will use this problem definition:

Given a maze, one entrance and one exit, find and print all possible ways someone can enter the maze and get out of it. The maze can have corridors (empty rooms) as well as walls (rooms you cannot go through).

As you can see from the problem definition, we have to find all the solutions. That is our first clue to use recursion and backtracking.

The idea for the solution: Recursion and Backtracking

We can describe the idea for the solution as follows:

Represent the maze as a bidimensional array (or a list of lists). Define one character to state that the room is empty and another for rooms that someone cannot go through.
There are four possible moves: forwards, backwards, left and right.
We have to iterate to all possible moves.
If the move is valid, we move. Now we change the starting point to the place we are right now and look for a solution starting on that new start-point.
Now we take a step back (backtracking) to check the rest of the possible moves.
If start == ends, we found a solution. So we can print the path in any format.

From step 4, you can see the definition of recursion that was described here: we are dividing our problem into smaller instances of the same problem.

Let’s say our maze is a matrix of 8×8. The entrance is at (0,0) and the exit is at (7,7). If we move to (0,1) and we rephrase the original problem as finding the way out from (0,1) instead of (0,0), we are reducing the size of the original problem. Now we have to check one room less.

We reduce more and more the size of the original problem by repeating the process several times.

The other condition we have to check is the stop condition. When does the recursion stop? If start == ends, it means we are already at the exit, so we stop the recursion and print the solution.

Python solution to the maze problem

I created some helpers to make the code cleaner and easy to understand.

Constants to store the size of the maze and the characters to print the solutions

I used the constants so I can easily modify the input parameters without modifying the main code (the actual recursive function).

size = 8
start_sign = '👤'
end_sign = '🚩'
right = '→'
left = '←'
up = '↑'
down = '↓'
empty_space = '_'
wall = '🀫'

Moves: an array holding the four possible moves

Here we have an array with the four possible moves. It will make our code cleaner because we now have four moves to check.

Notice I call the moves right, left, up and down. That is how you see the moves on the screen.

If you are inside a maze in the real world, the moves will be forward, backwards, left and right.

The array elements are dictionaries. Its values are constants that will allow us to check if we can move in that direction.

When the maze is in front of you (on the screen), you can go to the right if you add 1 to the column and keep on the same row. I represented the column by y and the row by x.

I defined the other moves similarly.

The other value in the dictionary (‘dir’: right) is the direction. That value will be used to render an arrow (check the constants on the previous section) to show the path.

moves = [
    {'x':0, 'y':1, 'dir': right}, # move right
    {'x': 0,'y': -1, 'dir': left}, # move left
    {'x': 1, 'y': 0, 'dir': down}, # move down 
    {'x': -1, 'y': 0, 'dir': up} # move up
]

Print the maze to see the solution

To print the maze we use a simple nested for-loop. Notice we need two conditions so we print a different character for the entrance and the exit.

def printMaze(lab, start, end):
    global size
    space = ' '
    for i in range(8):
        for j in range(8):
            if i == mstart.x and j == mstart.y:
                print(start_sign,  end=space)
            elif i == end.x and j == end.y:
                print(end_sign)
            else:
                print(lab[i][j],  end=space)
        print('')

A position class to handle positions in the maze

A simple class that represents a position by using two coordinates (x,y).

class Position:
    def __init__(self, x, y):
        self. x = x
        self.y = y
    def __eq__(self, other):
        return (self.x == other.x) and (self.y == other.y)

IsAValidMove helper

Before we move to a different position in the maze, we have to evaluate if the move is valid. We are checking here three conditions:

The row is valid after the move
The column is valid after the move
The place that we want to move to is empty

def isValidMove(start, move):
    return start.x + move['x']>=0 and start.x + move['x']<size \
        and start.y + move['y']>=0 and start.y + move['y']<size \
            and lab[start.x + move['x']][start.y + move['y']] == empty_space

findSolutions: using recursion and backtracking to solve the maze problem

This one is the main method, the one that do the backtracking to find all the solutions.

def findSolutions(lab, start, end):
    for move in moves:
        if isValidMove(start, move):
                lab[start.x][start.y ] = move['dir']
                start = Position(start.x + move['x'], start.y + move['y'])
                if start == end:
                    printMaze(lab, start, end)
                    input("Press Enter to continue...")
                findSolutions(lab, start, end)
                start = Position(start.x - move['x'], start.y - move['y'])
                lab[start.x][start.y ] = empty_space

A console app to test the implementation

This is a sample code to test teh rest of the implementation. Feel free to play with it.

Here I use ‘_’ and ‘🀫’ in the maze definition to look better on the post. But, you should use the constants empty_space and wall (check the section constants).

if __name__ == "__main__":
    lab = [['_', '_','_', '_', '_', '_', '_', '_'],
        ['_', '_','_', '🀫', '_', '_', '_', '_'],
        ['_', '🀫','_', '_', '🀫', '_', '_', '_'],
        ['_', '_','_', '_', '_', '_', '_', '_'],
        ['_', '_','_', '_', '_', '_', '_', '_'],
        ['_', '_','_', '🀫', '_', '_', '_', '_'],
        ['_', '_','_', '_', '_', '_', '🀫', '_'],
        ['_', '_','_', '_', '_', '_', '_', '_']]
        
    mstart = Position(0,0)
    end = Position(7,7)
    findSolutions(lab, mstart, end)

You can find all the code only on file (and other examples) in this link.