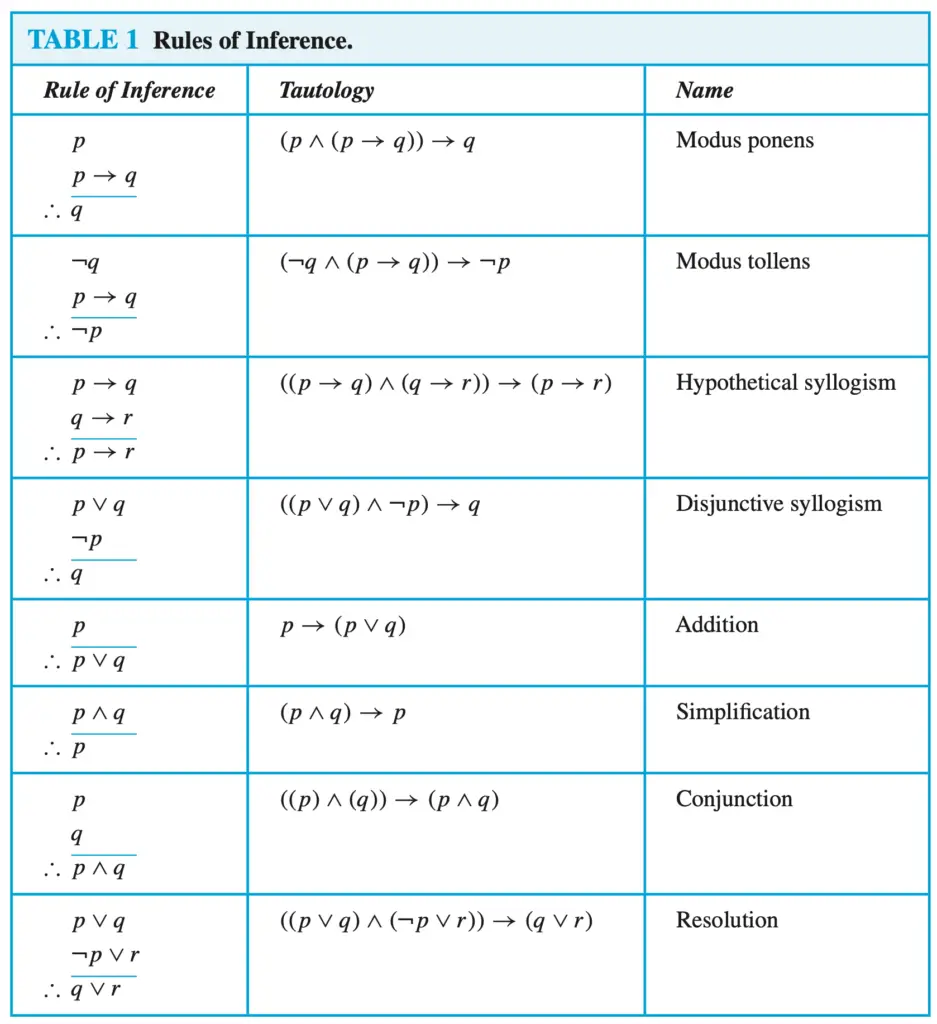
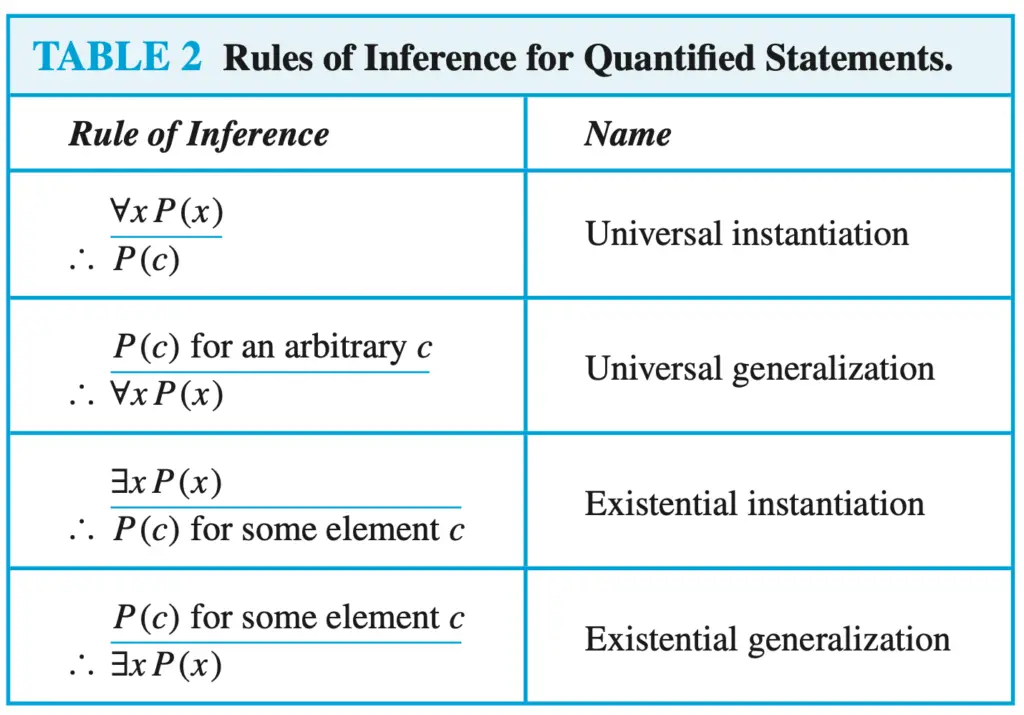
As with the previous examples, there are two main things we need to solve this exercise. First, we need to know the rules of inference so we can apply them. Second, we need to identify whether we must use propositional variables or predicates.
The first step will always be to translate the argument using propositional variables or predicates. Then we apply a sequence of rules of inferences to find out what conclusions we can draw from the premises.
Table of Contents
- a) “If I take the day off, it either rains or snows.” “I took Tuesday off or I took Thursday off.” “It was sunny on Tuesday.” “It did not snow on Thursday.”
- b) “If I eat spicy foods, then I have strange dreams.” “I have strange dreams if there is thunder while I sleep.” “I did not have strange dreams.”
- c) “I am either clever or lucky.” “I am not lucky.” “If I am lucky, then I will win the lottery.”
- d) “Every computer science major has a personal computer.” “Ralph does not have a personal computer.” “Ann has a personal computer.”
- e) “What is good for corporations is good for the United States.” “What is good for the United States is good for you.” “What is good for corporations is for you to buy lots of stuff.”
- f) “All rodents gnaw their food.” “Mice are rodents.” “Rabbits do not gnaw their food.” “Bats are not rodents.”
Remember to have the table with rules of inference at hand before start solving the exercises.
a) “If I take the day off, it either rains or snows.” “I took Tuesday off or I took Thursday off.” “It was sunny on Tuesday.” “It did not snow on Thursday.”
Let P(x)=”It was sunny on x”, Q(x)=”It snow on x”, R(x)=”I take x off”, S(x)=”It rain on x”
(1) R(x)->(S(x) ∨ Q(x)) Premise
(2) R(Tuesday) ∨ R(Thursday) Premise
(3) P(Tuesday) Premise
(4) ¬Q(Thursday) Premise
Because it was sunny on Tuesday, we can assume that it didn’t rain or snow that day.
(5) ¬ (S(Tuesday) ∨ Q(Tuesday) )
(6) R(Tuesday) -> (S(Tuesday) ∨ Q(Tuesday)) Universal instantiation using (1)
(7) ¬ R(Tuesday) Modus Tollens using (5) and (6)
(8) ¬ R(Thursday) Disjunctive syllogism using (2) and (7)
(9) R(Thursday) -> (S(Thursday) ∨ Q(Thursday)) Universal instantiation using (1)
(10) S(Thursday) ∨ Q(Thursday) Modus ponens using (8) and (9)
(11) S(Thursday) Disjunctive syllogism using (4) and (10)
Answer: I did not take Tuesday off. I took Thursday off. It rained or snowed on Thursday. It rained on Thursday.
b) “If I eat spicy foods, then I have strange dreams.” “I have strange dreams if there is thunder while I sleep.” “I did not have strange dreams.”
Let p=”I eat spicy food”, q=”I have strange dreams”, r=”there is thunder while I sleep”
(1) p->q Premise
(2) q->r Premise
(3) ¬q Premise
(4) ¬p Modus Tollens using (1) and (3)
(5) ¬r Modus Tollens using (2) and (3)
Answer: I didn’t eat spicy food. It didn’t thunder.
c) “I am either clever or lucky.” “I am not lucky.” “If I am lucky, then I will win the lottery.”
Let p=”I am clever”, q=”I am lucky”, r=”I will win the lottery”
(1) p ∨ q Premise
(2) ¬q Premise
(3) q -> r Premise
(4) p Disjunctive syllogism using (1) and (2)
We cannot draw another conclusion using (3).
Answer: I am clever
d) “Every computer science major has a personal computer.” “Ralph does not have a personal computer.” “Ann has a personal computer.”
Let P(x) = “x is a computer science major”, Q(x)=”x has a personal computer”
(1) ∀x (P(x)->Q(x)) Premise
(2) ¬Q(Ralph) Premise
(3) Q(Ann) Premise
(4) P(Ralph) -> Q(Ralph) Universal instantiation using (1)
(5) ¬P(Ralph). Modus tollens using (2) and (4)
(6) P(Ann) -> Q(Ann) Universal instantiation using (1)
We cannot draw any conclusion using (6) and (3)
Answer: Ralph is not a computer science major.
e) “What is good for corporations is good for the United States.” “What is good for the United States is good for you.” “What is good for corporations is for you to buy lots of stuff.”
Let P(x)=”x is good for corporations”, Q(x)=”x is good for the United States”, and R(x)=”x is good for you”
(1) P(x) -> Q(x) Premise
(2) Q(x) -> R(x) Premise
(3) P(for you buy a lot of stuff) Premise
(4) P(for you to buy a lot of stuff) -> Q(for you to buy a lot of stuff) universal instantiation using (1)
(5) Q(for you to buy a lot of stuff) -> R(for you to buy a lot of stuff) universal instantiation using (2)
(6) Q(for you to buy a lot of stuff). Modus Ponens using (3) and (4)
(7) R(for you to buy a lot of stuff). Modus Ponens using (5) and (6)
Answer: For you to buy a lot of stuff is good for the United States and it is good for you.
f) “All rodents gnaw their food.” “Mice are rodents.” “Rabbits do not gnaw their food.” “Bats are not rodents.”
Let P(x)=”x is a rodent”, Q(x)=”x gnaws its food”.
(1) ∀x(P(x) ->Q(x)) Premise
(2) P(Mouse) Premise
(3) ¬Q(Rabbit) Premise
(4) ¬P(Bat) Premise
(5) P(Mouse) -> Q(Mouse) Universal instantiation using (1)
(6) Q(Mouse) Modus Ponens using (2) and (5)
(7) P(Rabbit) -> Q(Rabbit) Universal instantiation using (1)
(8) ¬P(Rabbit) Modus Tollens using (3) and (7)
(9) P(Bat) -> Q(Batt) Universal instantiation using (1)
No relevant conclusion can be drawn from (9) and (4)
Answer: Mice gnaw their food. Rabbits are not rodents.
Related posts:
- What rule of inference is used in each of these arguments?
- Use rules of inference to show that the hypotheses “Randy works hard,” “If Randy works hard, then he is a dull boy,” and “If Randy is a dull boy, then he will not get the job” imply the conclusion “Randy will not get the job.”
- What rules of inference are used in this famous argument? “All men are mortal. Socrates is a man. Therefore, Socrates is mortal.”
- What are propositional equivalences in Discrete Mathematics?

