To solve exercises where you have to apply rules of inference, the first step is to know the rules of inference.
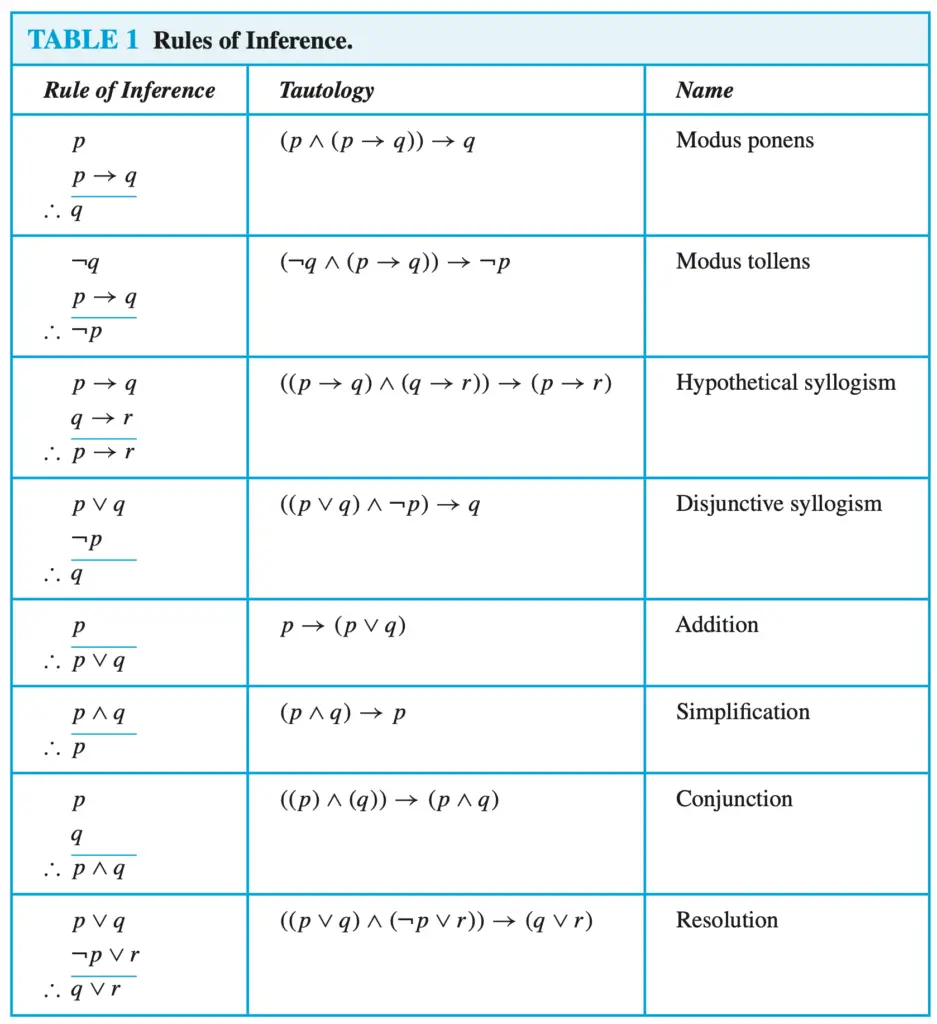
Once we know the rules, we can then start to apply them. So, let’s start solving the exercise.
“Randy works hard,” “If Randy works hard, then he is a dull boy,” and “If Randy is a dull boy, then he will not get the job” imply the conclusion “Randy will not get the job.”
Let p=” Randy works hard”, q=” Randy is a dull boy” and r=” Randy won’t get the job”.
Now, let’s write the hypothesis using the propositional variables p, q, and r.
(1) p Premise
(2) p->q Premise
(3) q->r Premise
And the conclusion will be r.
At this point, we must start applying the rules of inference from the table above in such a way that after one (or several) rules, we can get the conclusion r. This is also known as constructing an argument that shows that the premises lead to the desired conclusion (r in this case).
If we apply Hypothetical Syllogism to (2) and (3), we can conclude that p->r. We write that as follows:
(4) p->r Hypothetical Syllogism using (2) and (3),
(5) r Modus ponens using (1) and (4)
And with the previous steps, we constructed a valid argument that shows that the premises p, p->q, and q->r lead to the conclusion r.
Related posts:
- What rule of inference is used in each of these arguments?
- What rules of inference are used in this famous argument? “All men are mortal. Socrates is a man. Therefore, Socrates is mortal.”
- For each of these collections of premises, what relevant conclusion or conclusions can be drawn? Explain the rules of inference used to obtain each conclusion from the premises.
- What are propositional equivalences in Discrete Mathematics?
