Working with numbers is one of the first skills you should get when learning programming. It does not matter what programming language you are learning. This is always useful because it helps you to learn how algorithms work.
The short answer to this question is to use operations from mathematics: division, the remainder of division and subtraction. First, I’ll show how to get a single digit, using different restrictions, and then I’ll show how to print all the digits of the number without using strings. Let’s dive in on how to use these mathematical operations to extract the digits.
Extracting an individual digit using the remainder of the division and a loop
First, see the code below, then I’ll briefly describe the algorithm that extracts digits from a number without using strings.
def extract_digit(number, k):
c = 0
result = 0
while c <= k:
result = number % 10
number = int(number / 10)
c += 1
return result
So, what’s happening here?
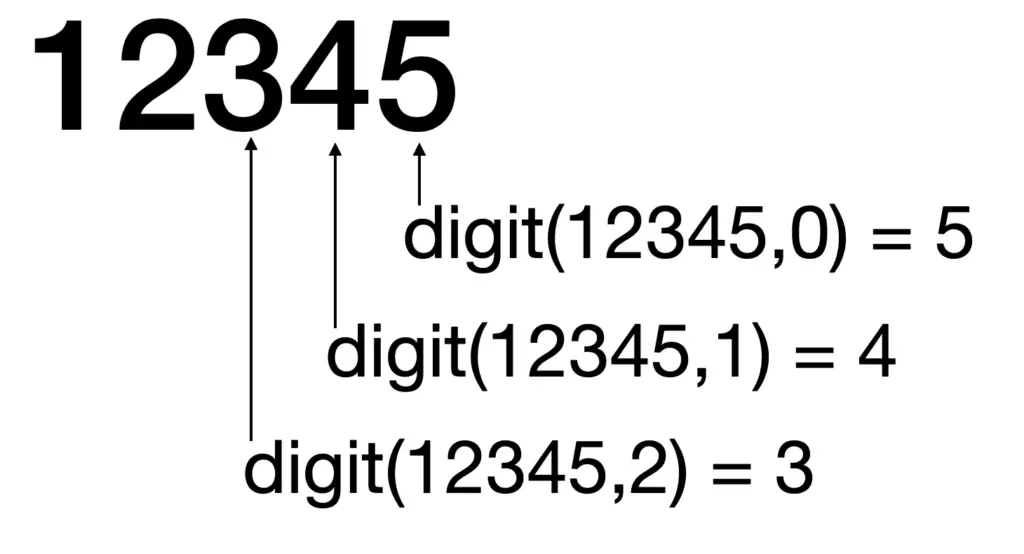
First, let’s analyse the integer division remainder operation (%, also called modulus in programming). This operation returns the remainder of the division. For instance, 12/10 = 1.2, and the remainder of the integer division equals 2, because 12 = 1*10 + 2.
The previous means that if we apply the % operator, we can get the last digit on a number.
Next question: how can we get the second?
See the answer in the following example.
123 / 10 = 12.3
If we take the integer part of that result (12) and apply the % operator again, we get 12 % 10 = 2. That’s how we obtain the second digit.
Next question, how can we get the third digit?
12345 / 10 = 1234.5
1234 / 10 = 123.4
123 % 10 = 3
Did you see the pattern?
To get the second digit, we divide by ten and then apply the operator %. After that, we get the third digit dividing by ten, two times, and then use the operator %.
To get the n-th digit, we divide n-1 times by ten and then use the modulus operator (%).
That is what the loop does. It calculates the remainder and then divides by ten until it is not necessary anymore.
That is why we need a loop in this case.
But, what if we have to do the same without using loops?
Extracting an individual digit without a loop
Here we have a new task, create a function without using loops, and it must give the same result as the previous one.
This type of task is very usual in programming. So, you will also see this type of limitation in interviews for programmers.
Yes, you guessed right. Programmers need to know how to solve this type of question.
If we review the algorithm explanation and implementation from the previous section, we can see that we are doing several divisions by ten. That’s what the loop is for, to repeat divisions by ten several times.
From basic maths, we know that if n / 10 = k, then k /10 = n/100. Therefore, instead of having a loop that divides by 10 several times, we can divide by 10^k, where k is the number of iterations in our previous loop-oriented solution.
def extract_digit_without_loops(number, k):
return int(number / (10 ** k)) % 10
As you can see, the code is shorter than before and still solves the problem without using strings. Cool! isn’t it?
Obtaining an individual digit without using the remainder of the division (%) operator
In this case, the approach is as follows:
- divide the number by 10
- rest the number from 10 times the result of the previous step
- that gives as result the last digit
- repeat using the result of step 1 as the original number
Example: number = 123, k =1
step 1. 123/10 = 12
step 2. 123 – 10*12 = 3 (k=0)
step 3. 23/10 = 2
step 4 (repeating step 1). 12/10 = 1
step 5 (repeating step 2). 12 – 10 * 1 = 2 (k=1)
step 5 (repeating step 1). 1/10 = 0
step 6 (repeating step 2). 1 – 10 * 0 = 1 (k=2)
Find the code below.
def extract_digit_without_reminder(number, k):
if k < 0:
return
while k >= 0:
result = int(number / 10)
digit = number - 10 * result
number = result
k = k - 1
return digit
Printing all the digits
To print all the digits at once, we can repeat extracting 1 digit until we have extracted them all.
Find the code below.
def print_all_digits(number):
while number > 0:
result = number % 10
number = int(number / 10)
print(result)
Great! Let’s see a summary of what we discussed in this article.
Testing all the implementations in a python console application
Notice in the code below, I used the same names of the code in the previous sections.
if __name__ == "__main__":
print('Using loops')
print(extract_digit(1234, 0))
print(extract_digit(1234, 1))
print('Without loops')
print(extract_digit_without_loops(1234, 0))
print(extract_digit_without_loops(1234, 1))
print('Without using remainder of the division')
print(extract_digit_without_reminder(1234, 0))
print(extract_digit_without_reminder(1234, 1))
print(extract_digit_without_reminder(1234, 2))
print(extract_digit_without_reminder(1234, 3))
print('Printing all digits from right to left')
print_all_digits(1234)
Summary
Sometimes, programmers have to solve problems under certain restrictions. The restrictions can be related to time complexity, spatial complexity, or the use of programming languages structures (loops and remainder of the division in the example we followed in this article).
When we have to solve a problem under certain restrictions, we have to be creative.
Being a programmer is a complex task because there is no algorithm to create algorithms that solve problems.
Therefore, any time we have to solve a problem, we have to use the knowledge we have from all areas of our life (mathematics, history, real-life, experiments, etc.) and be creative on how to use it.
You will also find out that the more problems you solve using programming, the more confident and creative you will get.
H@ppy coding!
Related posts:
Roadmap to learn programming: don’t learn a language
