The Binary Search Tree data structure implementation will help us to store data and to do efficient searches.
There are two main restrictions in this data structure:
- Every object to the left of the root is less than or equal to the root.
- Objects to the right of the root are greater than or equal to the root.
See the image bellow and check if the two conditions hold.
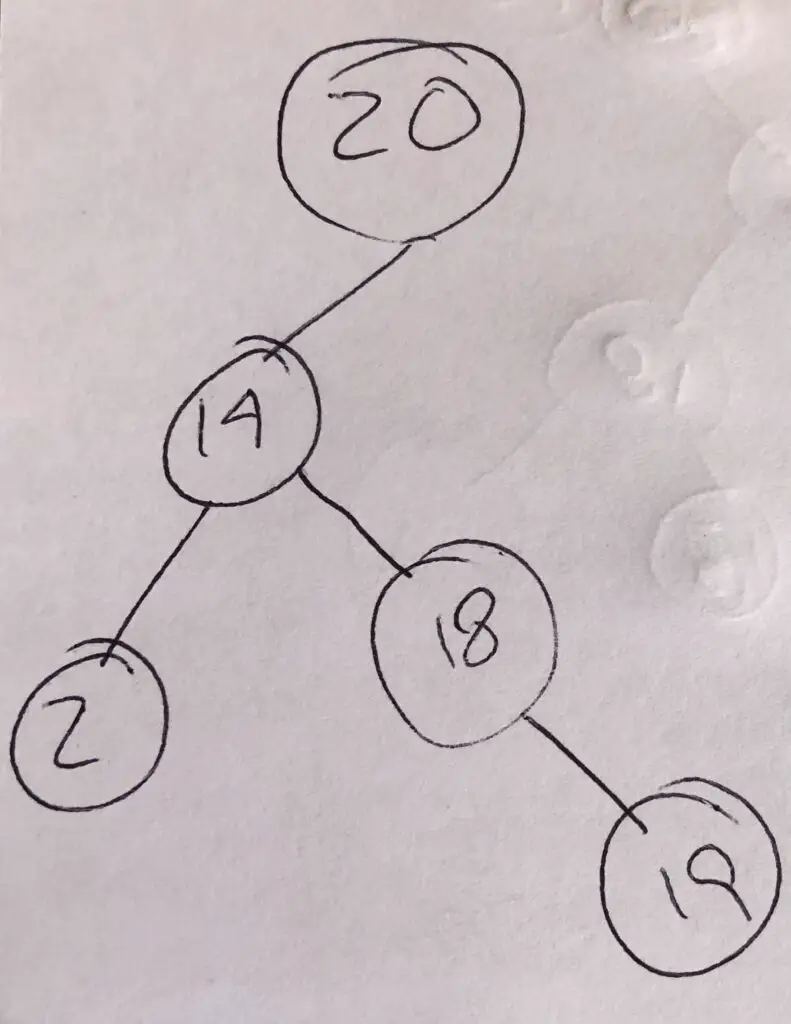
As I mention in another post, one of my favourite books to study data structure is Introduction to Algorithms by Cormen. If you need more information about data structures of algorithms, you will find it there.
Table of Contents
- Operations of the Binary Search Tree
- Java Implementation of the Binary Search Tree Data Structure
- Example of use of the BST
- Summary
Operations of the Binary Search Tree
As in other ADT’s (Graph, General Tree), there are certain operations that we must implement in a Binary Search Tree (BST):
- Search
- Minimum
- Maximum
- Predecessor
- Successor
- Insert
The name of the operations is self-explanatory.
Let’s go through an overview of the algorithms for each operation.
Search
Find below the implementation of the search method.
public BinarySearchTree<T> iterativeSearch(T info) {
BinarySearchTree<T> tree = this;
while (tree != null && info.compareTo(tree.root) != 0) {
if (info.compareTo(tree.root) < 0)
tree = tree.left;
else
tree = tree.right;
}
return tree;
}
The code above is self-explanatory.
If the node you are searching for is less than the root, you search on the left subtree. Otherwise, you must search on the right subtree.
The procedure should stop when one of two conditions are met:
- the tree is null. This means the node is not on the tree.
- The value on the root equals the value you are searching for.
Notice that in this case is an iterative implementation. As
Minimum-Maximum
To find a minimum, you must move all the way down to the left.
Because always, in a BST, values to the left are less than or equal to the value at the root.
For the maximum the procedure is almost the same, you just have to move to the right, because all the values to the right are higher or greater than the value at the root.
Successor-Predecessor
In this case, we must consider two situations.
First, If the left child of a node is not null, then the predecessor is the maximum value on the left subtree.
The second case is if the left subtree is null, then the predecessor is an ancestor (the lowest in the hierarchy) whose left child is also an ancestor.
For instance, consider the following figure. The successor of 19 is 20. Because 20 is the lowest ancestor whose left child (14) is also an ancestor of 19.
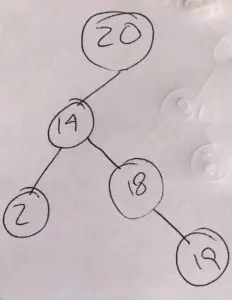
For the predecessor, we use a similar procedure, we just have to search on the opposite branch of the tree.
Insert
In a Binary Search Tree, we always insert a new node under a leaf.
The base case is if you are at a subtree without left or right children. If that is the case, you will insert the new subtree as the left child if the info on the root of the new node is less than or equal to the value on the root. Otherwise, you will add it as the right child.
If you are not at a leaf (a node whose left and right child equals null), you will ask if the node you want to insert is less than or equal to the value of the root; and if it is, you insert the new node (also a tree of one node) under the left subtree. Otherwise, you insert it under the right subtree.
Let’s jump straight to the Java implementation.
Java Implementation of the Binary Search Tree Data Structure
import java.util.LinkedList;
import java.util.List;
public class BinarySearchTree<T extends Comparable> {
private T root;
private BinarySearchTree<T> left;
private BinarySearchTree<T> right;
private BinarySearchTree<T> parent;
BinarySearchTree(T info) {
root = info;
left = null;
right = null;
parent = null;
}
public T Root() {
return root;
}
public boolean isLeaf() {
return left == null && right == null;
}
public void insert(BinarySearchTree<T> newTree) {
BinarySearchTree<T> parent = null;
BinarySearchTree<T> position =this;
while (position!=null){
parent = position;
if (newTree.root.compareTo(position.root)<0)
position = position.left;
else
position = position.right;
}
newTree.parent = parent;
if (newTree.root.compareTo(parent.root)<0)
parent.left = newTree;
else
parent.right = newTree;
}
public void insert(T info){
insert(new BinarySearchTree<>(info));
}
public List<T> preorder() {
return _preorder(new LinkedList<>());
}
private List<T> _preorder(List<T> result) {
result.add(root);
if (!isLeaf()) {
if (left != null)
left._preorder(result);
if (right != null)
right._preorder(result);
}
return result;
}
public List<T> inorder() {
return _inorder(new LinkedList<>());
}
private List<T> _inorder(List<T> result) {
if (isLeaf()) {
result.add(root);
} else {
if (left != null)
left._inorder(result);
result.add(root);
if (right != null)
right._inorder(result);
}
return result;
}
public List<T> postorder() {
return _postorder(new LinkedList<>());
}
private List<T> _postorder(List<T> result) {
if (left != null)
left._inorder(result);
if (right != null)
right._inorder(result);
result.add(root);
return result;
}
public int Height() {
if (isLeaf())
return 0;
int max = 0;
int h = left.Height();
int h1 = right.Height();
if (h < h1)
max = h1;
else
max = h;
return max + 1;
}
public BinarySearchTree<T> left() {
return left;
}
public BinarySearchTree<T> right() {
return right;
}
public T Succesor(BinarySearchTree<T> info){
if (info.right!=null)
return (T) info.right.Minimum();
BinarySearchTree<T> tree = info.parent;
while (tree!=null && info == tree.right){
info = tree;
tree = tree.parent;
}
if (tree==null)
return null;
return (T) tree.root;
}
public T Predecesor(BinarySearchTree<T> info){
if (info.left!=null)
return (T) info.left.Maximum();
BinarySearchTree<T> tree = info.parent;
while (tree!=null && info == tree.left){
info = tree;
tree = tree.parent;
}
if (tree==null)
return null;
return (T) tree.root;
}
public T Minimum() {
BinarySearchTree<T> tree = this;
while (tree.left != null)
tree = tree.left;
return (T) tree.root;
}
public T Maximum() {
BinarySearchTree<T> tree = this;
while (tree.right != null)
tree = tree.right;
return (T) tree.root;
}
public BinarySearchTree<T> search(T info) {
return _recursiveSearch(this, info);
}
private BinarySearchTree<T> _recursiveSearch(BinarySearchTree<T> tree, T info) {
if (tree == null || tree.root == info)
return tree;
if (info.compareTo(tree.root) < 0)
return _recursiveSearch(tree.left, info);
else
return _recursiveSearch(tree.right, info);
}
public BinarySearchTree<T> iterativeSearch(T info) {
BinarySearchTree<T> tree = this;
while (tree != null && info.compareTo(tree.root) != 0) {
if (info.compareTo(tree.root) < 0)
tree = tree.left;
else
tree = tree.right;
}
return tree;
}
}
Example of use of the BST
Find below an example of a Java Console Application that shows how to use the implementation of the Binary Search Tree.
public class BinarySearchTreeExample {
public static void main(String[] args) throws Exception {
BinarySearchTree<Integer> tree = new BinarySearchTree<>(5);
BinarySearchTree<Integer> one = new BinarySearchTree<>(1);
BinarySearchTree<Integer> six = new BinarySearchTree<>(6);
BinarySearchTree<Integer> eight = new BinarySearchTree<>(8);
tree.insert(4);
tree.insert(7);
//tree.insert(2);
tree.insert(eight);
tree.insert(one);
tree.insert(six);
tree.insert(50);
//BinaryTreeUtils.printTreeToConsole(tree, "");
System.out.println("Ordered list");
TreeUtils.printList(tree.inorder());
System.out.println("The sucessor of 6 is: ");
System.out.println(tree.Succesor(six));
System.out.println("The predecessor of 6 is: ");
System.out.println(tree.Predecesor(six));
System.out.println("The sucessor of 1 is: ");
System.out.println(tree.Succesor(one));
System.out.println("The predecessor of 1 is: ");
System.out.println(tree.Predecesor(one));
System.out.println("The sucessor of 8 is: ");
System.out.println(tree.Succesor(eight));
System.out.println("The minimum is " + tree.Minimum());
System.out.println("The maximun is " + tree.Maximum());
if ( tree.search(81) != null)
System.out.println("81 is in the tree");
else
System.out.println("81 is in NOT the tree");
}
}
After executing this sample Java Console Application, you will get the following result.

Summary
A binary search tree is a data structure that we can use to order elements of a collection.
One of the advantages of this data structure is its efficiency in searching elements within a collection.
Also, It can also be used to order an unordered collection of elements.
H@ppy coding!
