In this lesson, you are going to learn another important type of collection: multidimensional arrays in java.
Imagine we must create a program to represent a matrix. A matrix in mathematics, is a rectangular array or table of numbers, symbols, or expressions. In this example, we will consider only a matrix of integer numbers. The other type of elements can be represented in the same way, by changing the type of data that is stored.
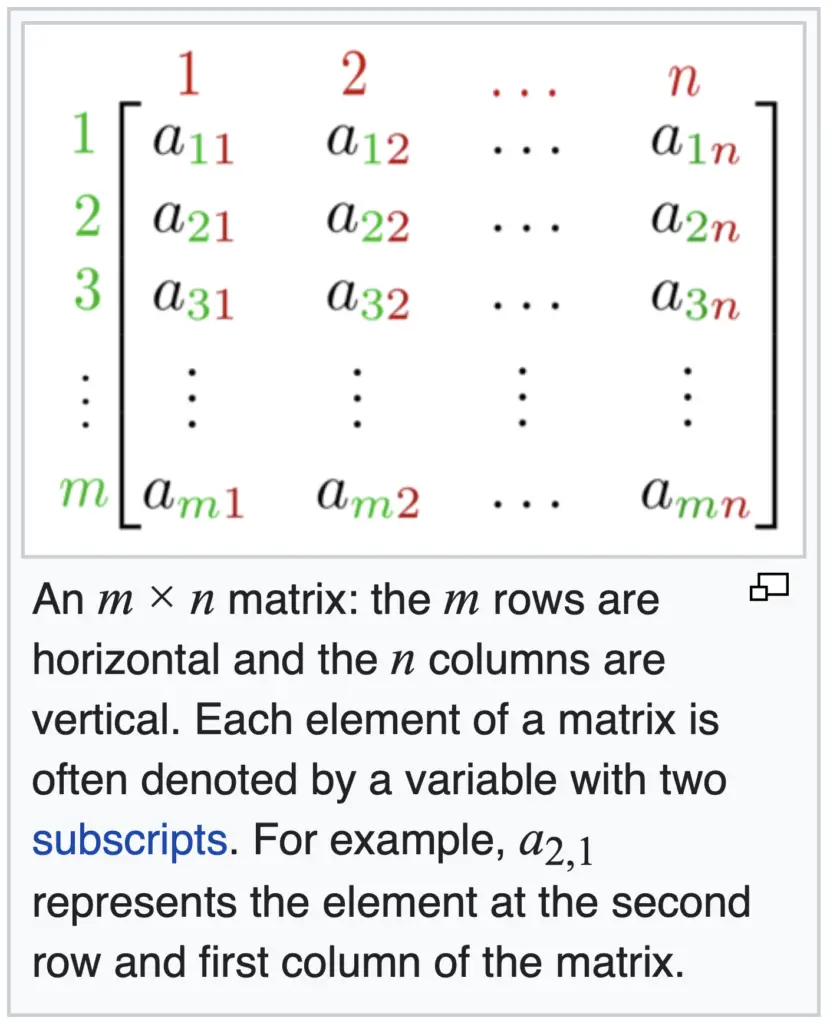
So, we the knowledge we until know, we can think on m several arrays, each of them will be used to represent a single row.
That is the basis for this new type of array.
Two-dimensional arrays in Java
From the definition and example in the previous section, we can see that a matrix is basically a table, in which each element has a position (defined by two subscripts or indices).
The position will be expressed as (row, column).
We can therefore model a matrix, as an array with two dimensions. One dimension is for the row and the other one is for the column.
In Java, we represent two-dimensional arrays as a kind of extension of unidimensional arrays. See the example below.
int matrix[][];
We can initialize this array in two ways.
int matrix[][] = {{1,2,3},
{4,5,6},
{7,8,9}};
The second way is used when we don’t know all the elements that will be in the matrix before the execution of the program.
int matrix [][]; matrix = new int[3][3]; matrix[0][0] = 1; matrix[0][1] = 2; matrix[0][3] = 3; ...
As you see in the second way, the same you assign a value to a specific cell of the matrix you can access that value and do something with it.
Accessing the elements of a two-dimensional array
So, if you want to print the second element of the second row, you can do it with the following code:
System.out.println(matrix[1][1]);
Notice that indices start at 0.
Now, how can we print all the elements of the matrix?
From the previous lesson, we know how to access (sum) every element of an array. See the code below.
int sum = 0;
for (int index=0; index< collection.length; index++){
sum = sum + collection[index];
}Printing all the elements in a two-dimensional array
If instead of summing the elements, we want to print them, we just change the block of instructions.
for (int index=0; index< collection.length; index++){
System.out.println(collection[index]);
}
In that way, we are going to print all the elements of the collection, in this case, a unidimensional array.
But we can see two-dimensional arrays as several unidimensional arrays. Also, we know already how to repeat a certain block of instructions.
This means that if we repeat the code that prints all the elements in a unidimensional array several times, we can solve our current problem of printing all the elements in the matrix or two-dimensional array.
Let’s see the code.
for (int row=0; row< matrix.length; row++){
for (int col=0; col<matrix[row].length; col++){
System.out.print(matrix[row][col]);
}
}
From the code below, you can see a for-loop within another for-loop. Don’t think about it like that.
Think this way, the block of instruction for the first for-loop is a code that prints every element of an array. Once we repeat that code several times, we print several arrays (several rows of the matrix).
On the second for-loop, you can see as a block of instruction that we are printing one element. The loop will print then, as many elements as the array have. Notice that each row of a matrix is a unidimensional array.
So, we are just using the indices row and cool to specify what row we want to iterate through (col<matrix[row].length😉 and then we print the specific element of the matrix (matrix[row][col] ).
When working with matrices, every time you want to access a specific element, you must use two subindices, first the row and then the column.
If you execute the code above, you will get as a result “123456789”.
How can we print this as a matrix?
We can use a simple trick, we print a space after each number, and after a row is printed (after the nested for-loop), we change the line in which we are printing. See the changes below.
public class Collections {
public static void main(String[] args) {
int matrix[][] = {{1,2,3},
{4,5,6},
{7,8,9}};
for (int row=0; row< matrix.length; row++){
for (int col=0; col<matrix[row].length; col++){
System.out.print(matrix[row][col] + " ");// add one space
}
System.out.println(); // change the line
}
}
}
If you execute the previous code, you will get the following as a result.

Lesson learned from this solution
To develop the previous solution, I followed an approach that we programmers follow most of the time.
Any time you have a problem, if you can modify it to another problem that you already know how to solve, you just solve the original problem.
We transformed the problem of printing each element of a matrix into the problem of printing several arrays or each row of a matrix.
Then we use the previous solution to print each element of an array, as our solution to print one row of the matrix. After that, we just repeated that solution as a block of instructions of a for-loop that iterates over each row of the matrix.
Problem solved!
So, my recommendation is any time you are trying to solve a problem, think first if you solved a similar problem before, and try to transform your current problem (or at least a part of it) into the one you already know how to solve.
A useful skill to create this new skill is to master the concept of abstraction in programming. You can read more about that here.
Multidimensional arrays
Sometimes, you need more than two dimensions to solve certain problems.
I won’t cover examples here because they are usually complex, and this is a beginner’s course.
However, it is good to know that they exist and can be used to solve problems using a programming language.
int collection []; // one dimension
int matrix [][]; // two dimensions
int matrix [][][]; // three dimensions
…
The examples are self-explanatory.
Just a remark, when you want to access one element of a one-dimensional (unidimensional) array you need to use one index. If the array has two dimensions, you need to use two indices (row, column) as seen in the example above.
For three dimensions, you must use three indices, and so on.
Summary
In this lesson, we study multidimensional (more than one dimension) arrays.
We can use them to represents collections of elements. We can still name them collection because any matrix, for instance, can be seen and modelled as a (unidimensional) array, in which each element (each row) is also an array.
H@appy coding!

