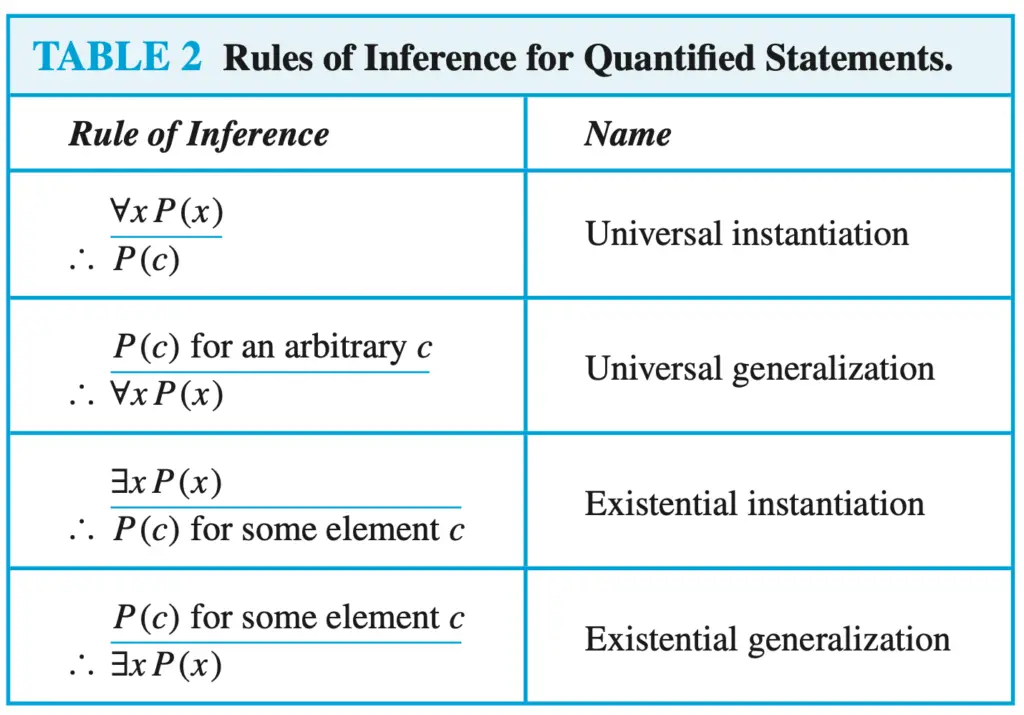
Like in other exercises related to rules of inferences, you first should know the basic rules of inferences before you can apply them to draw conclusions from certain premises.
If you still don’t know the rules of inference, make sure you open your textbook and have rules at hand so you can apply them.
Notice that is not necessary to memorize all the rules. If you solve enough exercises, you will find out that you know all the rules and you can apply them without effort.
Table of Contents
- a) “Doug, a student in this class, knows how to write programs in JAVA. Everyone who knows how to write programs in JAVA can get a high-paying job. Therefore, someone in this class can get a high-paying job.”
- b) “Somebody in this class enjoys whale watching. Every person who enjoys whale watching cares about ocean pollution. Therefore, there is a person in this class who cares about ocean pollution.”
- c) “Each of the 93 students in this class owns a personal computer. Everyone who owns a personal computer can use a word processing program. Therefore, Zeke, a student in this class, can use a word processing program.”
- d) “Everyone in New Jersey lives within 50 miles of the ocean. Someone in New Jersey has never seen the ocean. Therefore, someone who lives within 50 miles of the ocean has never seen the ocean.”
a) “Doug, a student in this class, knows how to write programs in JAVA. Everyone who knows how to write programs in JAVA can get a high-paying job. Therefore, someone in this class can get a high-paying job.”
Let:
- P(x)= “x is a student in this class”
- Q(x) = “x knows how to write programs in Java”
- R(x) = “x can get a high paying job”
Premises:
- P(Doug) ^ Q(Doug) premise
- ∀x (Q(x) -> R(x) ) premise
- Q(Doug) -> R(Doug) universal instantiation (2)
- Q(Doug) simplification (1)
- R(Doug) Modus ponens 3 and 4
- P(Doug) premise
- P(Doug) ^ R(Doug) conjunction 5 and 6
- ∃x (P(x) ^ R(x)) Existential generalization using 7
b) “Somebody in this class enjoys whale watching. Every person who enjoys whale watching cares about ocean pollution. Therefore, there is a person in this class who cares about ocean pollution.”
Let:
- P(x) = “x is in this class”
- Q(x) = “x enjoys whale watching”
- R(x) = “x cares about ocean pollution”
- ∃x (P(x) ^ Q(x)) premise
- ∀x (Q(x) -> R(x)) premise
- P(y) ^ Q(y) Existential instantiation
- Q(y) simplification using 3
- P(y) simplification using 3
- Q(y) -> R(y) universal instantiation using 2
- R(y) modus ponens using 5 and 6
- P(y) ^ R(y) conjunction using 5 and 7
- ∃x (P(x) ^ R(x)) Existential generalization using 7
c) “Each of the 93 students in this class owns a personal computer. Everyone who owns a personal computer can use a word processing program. Therefore, Zeke, a student in this class, can use a word processing program.”
Let:
- P(x) = “x is student in this class”
- Q(x) = “x owns a personal computer”
- R(x) = “x can use a word processing program”
- ∀x (P(x) -> Q(x)) premise
- ∀x (Q(x) -> R(x)) premise
- P(Zeke) premise
- P(Zeke) -> Q(Zeke) Universal instantiation using 1
- Q(Zeke) -> R(Zeke) Universal instantiation using 2
- P(Zeke) -> R(Zeke) hypothetical syllogism using 4 and 5
- R(Zeke) Modus ponens using 3 and 6
d) “Everyone in New Jersey lives within 50 miles of the ocean. Someone in New Jersey has never seen the ocean. Therefore, someone who lives within 50 miles of the ocean has never seen the ocean.”
Let:
- P(x) = “x lives in New Jersey”
- Q(x) = “x lives within 50 miles of the ocean”
- R(x) = “x has never seen the ocean”
- ∀x (P(x) -> Q(x)) premise
- ∃x (P(x) ^ R(x)) premise
- P(y) -> Q(y) Universal instantiation using 1
- P(y) ^ R(y) Existential instantiation using 2
- P(y) simplification using 4
- R(y) simplification using 4
- Q(y) modus ponens using 3 and 5
- Q(y) ^ R(y) conjunction using 6 and 7
- ∃x (Q(x) ^ R(x)) Existential generalization using 8
Related posts:
- What rule of inference is used in each of these arguments?
- Use rules of inference to show that the hypotheses “Randy works hard,” “If Randy works hard, then he is a dull boy,” and “If Randy is a dull boy, then he will not get the job” imply the conclusion “Randy will not get the job.”
- What rules of inference are used in this famous argument? “All men are mortal. Socrates is a man. Therefore, Socrates is mortal.”
- For each of these collections of premises, what relevant conclusion or conclusions can be drawn? Explain the rules of inference used to obtain each conclusion from the premises.
