The sequence 1 4 9 17 in python: a tricky pattern

Sequences are a powerful tool in mathematics and in programming. In this post, you will learn how to print a pattern with two sequences in python: the sequence 1 4 9 17 and an easier sequence that just add 2 to the previous value.

If you want yo read more about sequences in mathematics, you can read this post.

The following picture shows the pattern we want to print.

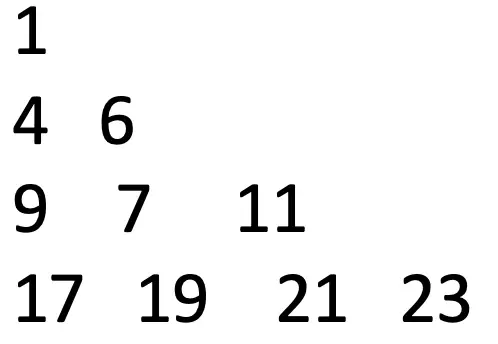
The sequence 1 4 9 17 in python: a tricky pattern — Write a program in python that prints this pattern

We are going to use a strategy that is commonly used in algorithm design (and also in many other areas: mathematics, daily life, etc.): Divide and Conquer.

Let’s divide our problem. We clearly have to sequences to calculate. One sequence for the first column: 1 4 9 17. The second sequence is for each row, for instance 4 6, 9 7 11, and so on.

Let’s start with the easier one.

Row sequence

If we look at second row, we can see that the second number is the first one plus 2.

Now we check the next row, the second number is the first one plus 2, and the third number is the second plus 2. The same happen in the next row.

We just identified our first pattern. We can just calculate the next number by adding to the current one.

Also notice the number of values on each row. The first row has 1 value, the second row have 2, the third one has three and so on.

That is our second pattern. Now that we are clear on the sequences let’s implement the row sequences.

def print_row(row, first_value):
    seq = first_value 
    for col in range(row+1): 
        print (seq, end=' ')
        seq = seq + 2
    print('')

if __name__=='__main__':
    print_row(0, 1)
    print_row(1, 4)
    print_row(2, 9)
    print_row(3, 17)

If you try the previous code, you will see that we printed the pattern. But we are not calculating yet the first value of each row. That is our next step.

The technique Divide and Conquer, gives us the ability of concentrating in one single problem at a time.

In this case, we just printed the rows without being worried about how to calculate the first element of each row.

After we see that our code is printing each row properly, let’s take care of calculating the first element of each row.

First column sequence: 1 4 9 17

This one is the tricky one.

The difference between the first one and the second one is 3. Then, between the second and third ones is 5, the next one is 8.

Here, it is not easy to see the pattern like in the previous case.

Let’s write the sequence in the following way:

4 = 1 + 3

9 = 4 + 5

17 = 9 + 8

29 = 17 + 12, 29 should be the next term of the sequence.

In this way, we can express the sequence that we have to calculate.

Now our problem is how to calculate the sequence 3 5 8. Once we know how to do that, we just have a simple arithmetic problem.

Looking at our new sequence, the difference between the first one and the second (3 and 5) is 2. Then, the difference between the second and third (5 and 8) is 3, next difference (8 and 12) is 4, and so on.

This pattern is very easy to implement because we just have to add 1 to the previous difference and we can get the next value.

Let’s see the python code.

def pattern(rows): # rows is the number of rows we want to print
    start = 1 # this is the sequence 1 4 9 17
    aux_sequence = 2  # this is the sequence 3 5 8 12
    inc = 1 # This is used to calculate each element of the auxiliar sequence
            # for the next value, you have to add 1 to the difference of the previous two values
    for row in range(rows):  
        aux_sequence += inc # seq 3 is used to calculate the numbers on the main sequence
        inc += 1  
        print_row(row, start)
        
        start += aux_sequence  # new element on the sequence that represents the first element
                            # of each row, we increment the number by using seq3 + 1    

if __name__=='__main__':
   pattern(5)

The sequence 1 4 9 17 29 in python: a tricky pattern

Remarks

Divide and Conquer is a powerful technique that will help us to solve many complex problems by dividing them in several problems, and then combine the solutions to solve the original problem.

Sometimes, programming or coding tasks are not mainly about coding itself, but about thinking creatively and problem-solving oriented.

Related posts:

H@ppy coding