The Pascal Triangle is a well-known number pattern in mathematics. Because of the way it is created, it is helpful to practice loops and strings. Let’s see how to implement the Pascal Triangle in Python.
In this case, we can practice loops by creating each row of the triangle. We can also practice strings because we need to have some spaces at the beginning of each row. The number of spaces will vary depending on the row we are printing.
The Pascal Triangle
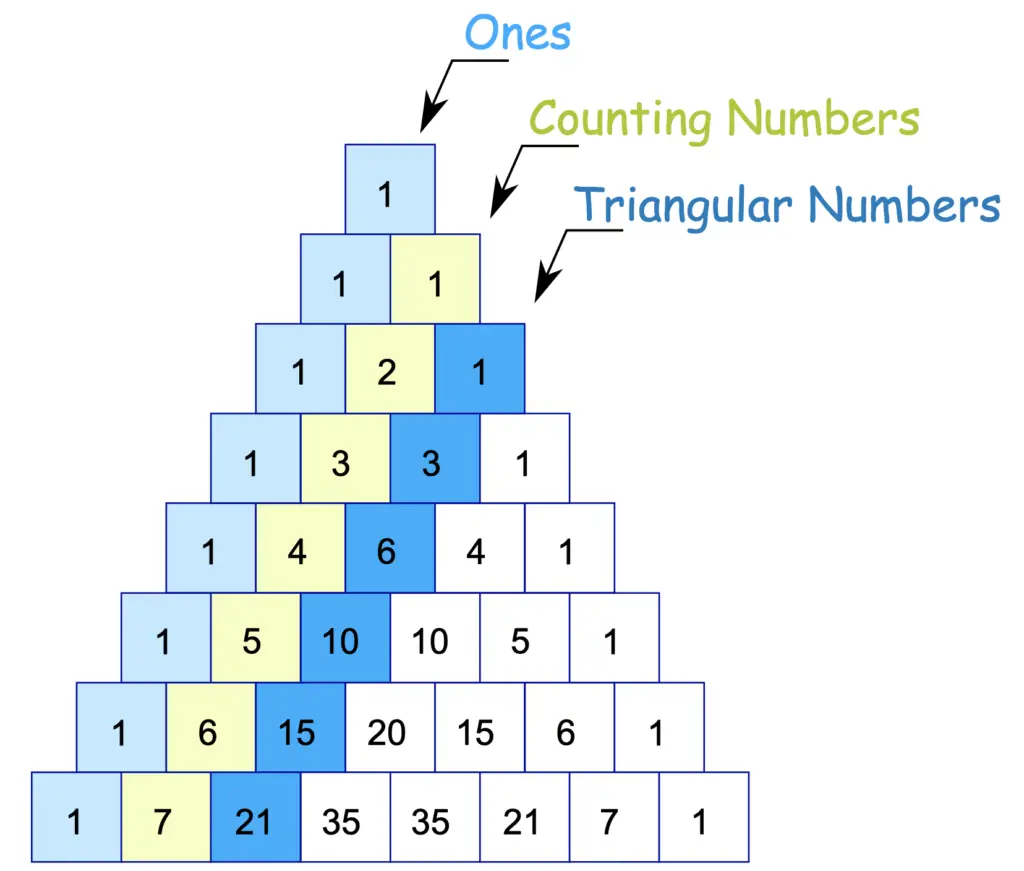
In this link, you can see all the patterns you can find in a Pascal Triangle.
One of the ways we can use to calculate each value is to use the binomial coefficient.
Python Implementation
We can create a python code to print the Pascal Triangle in different ways.
In this article, we are going to use the binomial coefficients.
To focus on the use of loops and strings we are going to use this way of calculation. However, it is not the best way because of the temporal complexity of the code.
To calculate the binomial coefficient, we need to calculate the factorial of three numbers.
So, let’s start implementing a function that will return the factorial.
Factorial of n in Python
If you want to learn more about the factorial you can check this link.
def factorial(n):
f = 1
while n>1:
f = f * n
n = n -1
return fIn this example, we can see how to use a while-loop. The while loop is called a precondition loop. It means that if the condition does not hold, the instructions within the loop won’t be executed.
There also post-condition loops. That type of loops will execute the instructions within the loop and then check if a condition holds. If it holds, then the instructions within the loop will be repeated. In this case, the instructions will always be executed at least once.
Now let’s calculate the binomial coefficient.
Binomial coefficient function in Python
To implement a function to calculate this value, we first need to know the formula.
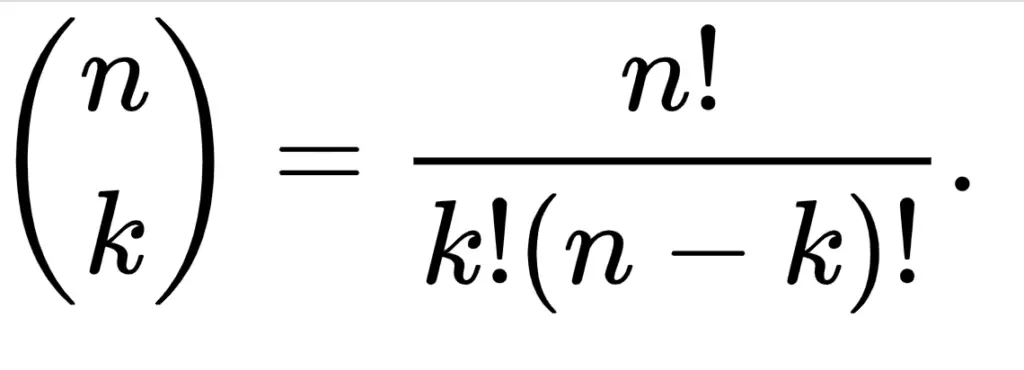
def binomial_coefficient(n, k):
return factorial(n)/(factorial(k)*factorial(n-k))The previous is a straightforward implementation. We just translate the formula to python.
Here you only need to use parenthesis to ensure that the multiplication in the denominator is done before the division.
Now, we are ready to start printing the triangle.
Function in python to print the Pascal Triangle using the binomial coefficient
In our case, n and k (from the binomial coefficient formula) will be the row and column of the value we have to calculate. Rows and columns will start in 0.
def print_pascal_triangle(n):
for row in range(n):
for col in range(row+1):
#calculate the value for col
val = int(binomial_coeficient(row, col))
print (val, end=space)
print('') # change to the new line
In the previous code, you can see another type of loop. In this case, we are using an iterator. It is a variable that will take values in a sequence of possible values.
In the previous example, the sequence is a range that goes from 0 until n (not including n) in the first loop.
Also, we have here an example of nested loops. Meaning there is one loop inside of the other one. Nested loops are helpful when we have to deal with multiple dimensions. In this case, we have a dimension for the rows and another one for the columns.
If we execute this code, we are going to get the following result.

Great! We calculated all the values on each row in the right way. But it does not have the shape we need.
We have to print the triangle as follows:

How can we do it?
One way is to use strings. We can add empty spaces before (and after) each number to get the desired shape.
Using strings ro print the Pascal Triangle in Python.
Let’s modify the code to add spaces (as much as we need) in front of each row.
space = ' ' one empty space
def print_pascal_triangle(n):
for row in range(n):
# row i have i+1 cols
left_spaces = space * (n-row)
# add spaces at the begening of the row to have the
#shape of the triangle
print(left_spaces, end=space)
for col in range(row+1):
#calculate the value for col
val = int(binomial_coeficient(row, col))
#adjust the number to three spaces
print ( val, end=space)
print('') # change to the new line
With the previous implementation, we can get the following result.

That’s great. This the pascal triangle for n = 5. Let’s print the triangle for n = 10.

Wait! That does not look right. It is because we have numbers with 1, 2 and 3 digits. Values with a different number of digits need a different space to be printed. That is why the rows with 2-digit numbers are longer than they should be. The same happens with the rows that have 3 digit numbers.
How we fix this? the answer is: by using strings.
Let’s reserve three spaces for each value we are going to print. If the value has one digit, we add 1 space at the beginning and 1 at the end. If the value has 2 digits, we add 1 space at the end.
We are going to use an auxiliar function to do the previous steps.
def add_spaces_to_val(val):
sval = str(val)
if len(sval) == 1:
sval = ' ' + sval + ' '
elif len(sval) == 2:
sval = sval + ' '
return sval
After that, we just need to print what the previous function returns, instead of the value without spaces.
space = ' ' # three spaces for each
def print_pascal_triangle(n):
for row in range(n):
# row i have i+1 cols
left_spaces = space * (n-row) # add spaces as needed
# add spaces at the begening of the row to have the
#shape of the triangle
print(left_spaces, end=space)
for col in range(row+1):
#calculate the value for col
val = int(binomial_coeficient(row, col))
#adjust the number to three spaces
print ( add_spaces_to_val(val), end=space)
print('') # change to the new line
Let’s see the result.
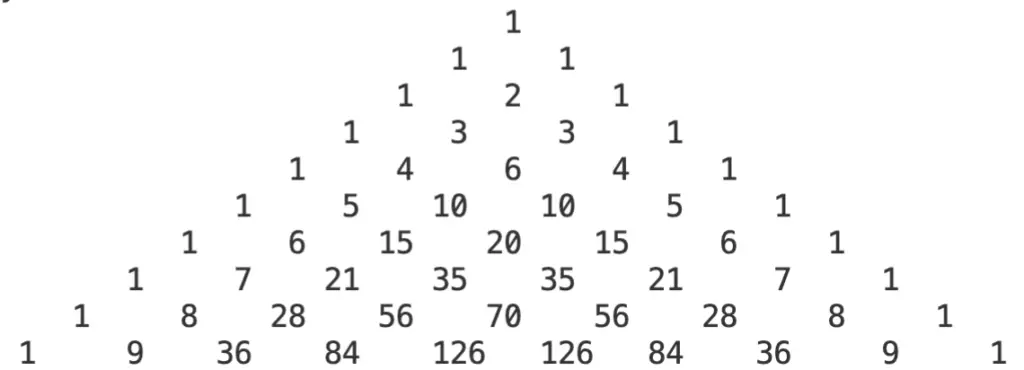
Yes! The triangle now looks the way it supposed to looks.
To add support for bigger numbers, you can follow the same approach. Add empty spaces as you need them.
Find the complete code here.
So, I hope this was useful for you and you already try it.
Practice more by adding support for bigger numbers and share your results in the comments.
Find more python examples here.
H@ppy coding!
Related posts:
