To prove the associative laws, we need to use the truth table for conjunctions and disjunctions.
Truth tables for conjunction and disjunctions
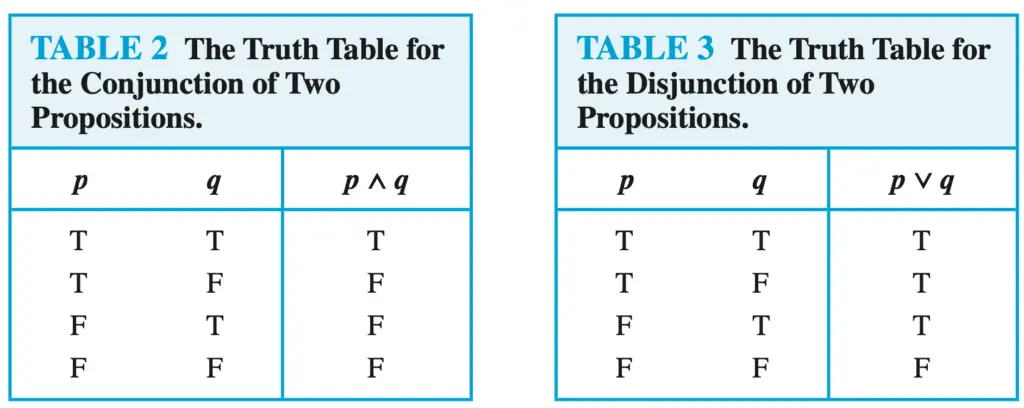
Now we can start solving the exercise.
a) (p∨q)∨r ≡p∨(q∨r)
As in previous examples, let’s examine what will be the structure of the truth table we must create.
There are three propositional variables, so we will have 8 rows.
Also, we have four compound propositions, so we need 7 (3 variables plus 4 compound propositions) columns.
| p | q | r | p∨q | (p∨q)∨r | q∨r | p∨(q∨r) |
| T | T | T | T | T | T | T |
| T | T | F | T | T | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | T | F | T |
| F | T | T | T | T | T | T |
| F | T | F | T | T | T | T |
| F | F | T | F | T | T | T |
| F | F | F | F | F | F | F |
Notice that to find the truth value in each compound proposition, we need to use the truth tables for conjunction or disjunctions. For instance, in the first row p∨q has value T, because according the truth table for the disjunction of two propositions, TvT is T.
According to the table above, (p∨q)∨r is logically equivalent to p∨(q∨r) because they have the same truth values.
b) (p∧q)∧r ≡p∧(q∧r)
Following a similar reasoning to the previous exercise, we can conclude that we need a table with 7 columns and 8 rows.
| p | q | r | p∧q | (p∧q)∧r | q∧r | p∧ (q∧r) |
| T | T | T | T | T | T | T |
| T | T | F | T | F | F | F |
| T | F | T | F | F | F | F |
| T | F | F | F | F | F | F |
| F | T | T | F | F | T | F |
| F | T | F | F | F | F | F |
| F | F | T | F | F | F | F |
| F | F | F | F | F | F | F |
Notice that to find the truth value in each compound proposition, we need to use the truth tables for the conjunction of two propositions. For instance, in the third row p∧q has value F, because according the truth table for the disjunction of two propositions, T∧F is F.
In the same way, in the first row, p∧ (q∧r) has the value T because, in the first row, p is T and q∧r is also T, then T∧T is T according to the truth table for the conjunction of two propositions.
According to the table above, (p∧q)∧r is logically equivalent to p∧ (q∧r) because they have the same truth values.
Related posts:
- What are propositional equivalences in Discrete Mathematics?
- Use truth tables to verify these equivalences (Ex 1. pp. 34 from the textbook)
- Show that ¬(¬p) and p are logically equivalent (Ex 2. pp. 34 from the textbook)
- Use a truth table to verify the first De Morgan law (Ex. 6 pp. 34 from the textbook)
- Show that p → q and ¬q → ¬p are logically equivalent (Ex 18 pp 35 from the textbook)
- Show that p↔ q and (p∧q)∨(¬p∧¬q) are logically equivalent
