In this example, we should use a truth table to verify each propositional equivalence.
Because in this case the exercises only involve the use of conjunctions (∧) and disjunctions (∧), we start by having at hand (or in memory) the truth tables for those logical operators.
Table of Contents
- Truth tables for conjunction and disjunction
- a) p∧T≡p
- b) p∨F≡p
- c) p∧F≡F
- d) p∨T≡T
- e) p∨p≡p
- f) p∧p≡p
- Summary
Truth tables for conjunction and disjunction
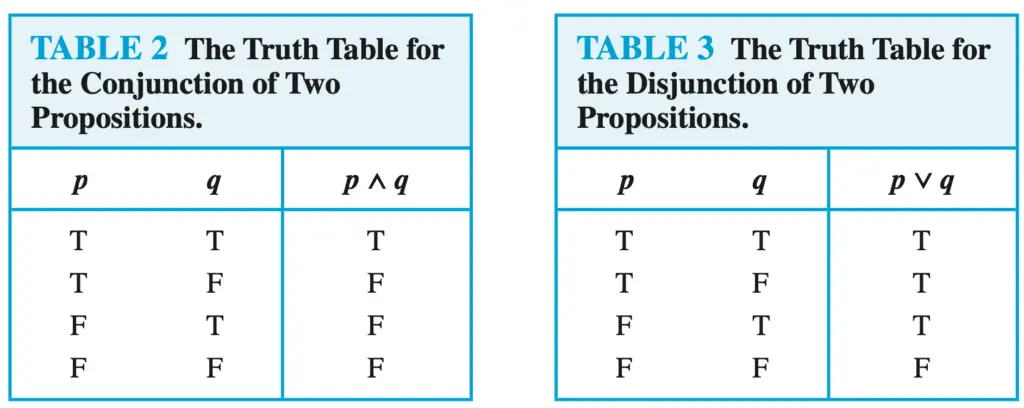
a) p∧T≡p
In this case, we only have one propositional variable (p), the other value is fixed to T. So, we only will need two columns and two rows.
| p | P∧T |
| T | T |
| F | F |
From the figure above, we can see that T ∧ T is T and F∧F is also T.
According to the truth table above, we can state that p∧T is logically equivalent (≡) to p because they have the same truth values.
b) p∨F≡p
This example is similar to the first one, with only one propositional variable and a fixed value, so the table will have two columns and two rows.
Also, we use the truth table for disjunction (see figure above) to determine the truth values in the first column of the table below.
| p | p∨F |
| T | T |
| F | F |
According to the truth table above, we can state that p∨F is logically equivalent (≡) to p because they have the same truth values.
Notice that is not enough to create the truth table, you need to state a conclusion (the sentence above) and explain why you arrived at that conclusion (the second part of the sentence).
c) p∧F≡F
| p | p∧F |
| T | F |
| F | F |
From the truth table above, we can state that p is not logically equivalent to p∧F because they don’t have the same truth values (see the first row).
Again, see that you need to state your conclusion and justify it, it is not enough to create the truth table.
d) p∨T≡T
| p | p∨T |
| T | T |
| F | T |
From the truth table above, we can state that p is not logically equivalent to p∨T, because they don’t have the same truth values (see the second row).
e) p∨p≡p
| p | p∨p |
| T | T |
| F | T |
From the truth table above, we can state that p is not logically equivalent to p∨p, because they don’t have the same truth values (see the second row).
f) p∧p≡p
| p | p∧p |
| T | T |
| F | F |
From the truth table above, we can state that p is logically equivalent to p∧p, because they don’t have the same truth values (see the first row).
In this example, we just prove one of the idempotent laws.
Summary
When you are asked to prove that a certain proposition is logically equivalent to another one, you can follow these steps:
- Make sure you know (or have at hand) the truth tables for the logical operators involved in the compound proposition (∧,∨,¬, etc.).
- Create a table: 1 column for each propositional variable and 1 column for each compound proposition.
- Make sure you use all possible combinations of truth values for the variables. For instance, 1 propositional variable can have two truth values (T and F), but when you use two propositional variables, you should have 4 rows (combining T and F for two variables), for three variables will be 8 rows, and so on.
- When the table is complete, state your conclusion and justify why that one is your conclusion.
Related posts:
- What are propositional equivalences in Discrete Mathematics?
- Show that ¬(¬p) and p are logically equivalent (Ex. 2 pp 34 from the textbook)
- Use truth tables to verify the associative laws (Ex. 4 pp. 34 from the textbook)
- Use a truth table to verify the first De Morgan law (Ex. 6 pp. 34 from the textbook)
- Show that p → q and ¬q → ¬p are logically equivalent (Ex. 18 pp 35 from the textbook)
- Show that p↔ q and (p∧q)∨(¬p∧¬q) are logically equivalent
