As in the previous examples, first, we need to know the rules of inferences.
In this example, you need to realize that you must use predicates instead of propositional variables. Because of that, we also need the rules of inference for quantified statements.
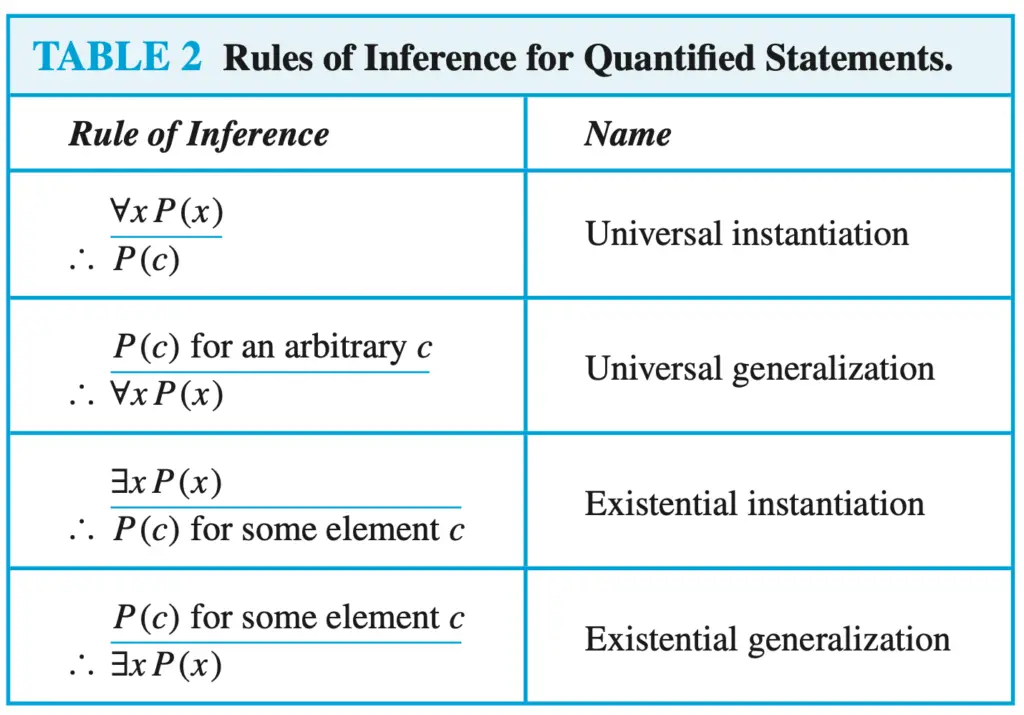
Let’s use predicates to represent the argument, then we will apply the rules of inference.
Let P(x)=“x is mortal” and Q(x)=”x is a man”.
Now we can rewrite the argument as follows:
(1)∀x (Q(x)->P(x)) Premise (all men are mortal, or, if x is man, then x is mortal)
(2) Q(Socrates) Premise (Socrates is a man)
Therefore,
P(Socrates) Conclusion (Socrates is mortal)
Let’s start applying the rules of inference.
(3) Q(Socrates) -> P(Socrates) Universal instantiation using (1)
(4) P(Socrates) Modus ponens using (2) and (3)
A common mistake I see students make in this type of exercise is using propositional variables instead of predicates. You need to know that if you don’t use predicates, your solution will be wrong. So, probably the most important thing you need to do to get this type of exercise right is to identify that you need to use predicates instead of propositional variables.
Related posts:
- What rule of inference is used in each of these arguments?
- Use rules of inference to show that the hypotheses “Randy works hard,” “If Randy works hard, then he is a dull boy,” and “If Randy is a dull boy, then he will not get the job” imply the conclusion “Randy will not get the job.”
- For each of these collections of premises, what relevant conclusion or conclusions can be drawn? Explain the rules of inference used to obtain each conclusion from the premises.
- What are propositional equivalences in Discrete Mathematics?
